MEASURES OF DISPERSION
We have seen how to get an average for a given distribution. The average represents a given distribution but when we want to study the given distribution, knowing only the average value is not enough. For instance, though it is useful to have an average of wages of workers in a factory, this value may not be sufficient to indicate the wage conditions in the factory. We should also know the differences in individual wages. Average does not give the idea about the spread or scatter of the data.
The same average may be found in two distributions yet they may differ widely in the scatter of their values. In the following examples we have three series. The arithmetic mean and median are the same for all the three.
A
|
B
|
C
|
60
60
60
60
60
|
50
55
60
65
70
|
0
30
60
90
120
|
Here se can see that though the averages are the same, the three series are widely different from each other. If we consider only the average, conclusion will be misleading as the same number will represent the three series.
The first series A has all equal observations. There is no variability. The observations in the series B differ by 5, while the difference between two consecutive observations in series C is 30. It is clear that the variability or scatter in series C is more than that in series B. In order to estimate to what extent the data vary from the average and to measure the spread or scatter of the data we compute measures of dispersion so that by referring to a single number we can find whether a distribution is compact or spread out.
Dispersion is an important characteristic and must be measured for the information it gives about the data. Two students may have the same average of marks. But one may be having marks near the average in all the subjects while the other may be having low marks in some subjects and very high marks in others. A manufacturer wants to control the quality of his product. He is interested in providing articles with uniform quality and therefore wants to prevent variability. For him uniformly high quality is better than high average. A manufacturer who produces electric bulbs will be happier with an average life of 1600 hours for his bulbs with uniform quality than an average life of 1700 hours with some bulbs lasting for less than 1000 hours and some for more than 2000 hours.
For measuring dispersion we have various measures and each of them has different characteristics. As in the case of averages, measures of dispersion also should have some qualities so that they give proper idea about the scatter of the data. The following are the characteristics of a good measure of dispersion.
- It should be rigidly defined.
- It should be based on all the observations.
- It should be easy to calculate and understand.
- It should be capable of further algebraic treatment.
- It should not be affected much by sampling fluctuations.
Measures of Dispersion
Absolute Measures Relative Measures
1. Range 1. Coefficient of Range
2. Quartile Deviation 2. Coefficient of Quartile Deviation
3. Mean Deviation 3. Coefficient of Mean Deviation
4. Standard Deviation 4. Coefficient of Variation
Range
An elementary measure of dispersion is range. It is the easiest of all measures of dispersion. It is defined as the difference between the highest and the lowest values taken by the variable.
i.e. Range = Maximum value – Minimum value
The corresponding relative measure is given by
.
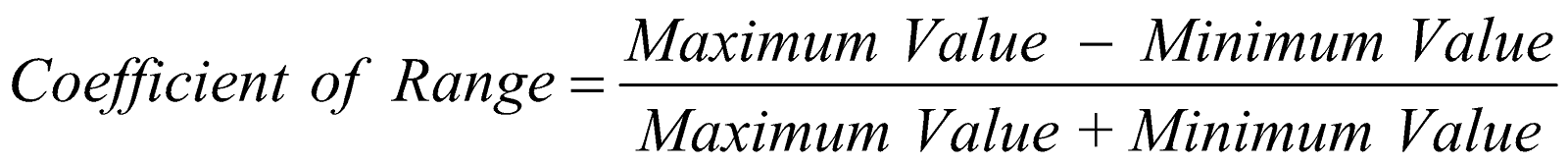Example: Calculate the range for the following data giving the daily sales of a shop for a week.
Sales in Rs.: 160, 130, 125, 127, 143, 150, 155
Here the lowest value is Rs.125 and the highest value is Rs.160.
Range = 160 – 125 = 35.
Range indicates nothing concerning the usual spread of the items. Therefore it is most useful when it is known that the extreme items are not exceptional in nature. Stock prices and interest rates are often stated in terms of their range. Range is used in statistical quality control to study the variation in quality of manufactured units. Saving in computation time is an important factor in favour of range. However range is not suitable for precise studies. It is only a rough measure of dispersion.
QUARTILE DEVIATION
Range is affected by extreme values. To avoid this we consider the range of the middle 50 per cent of the observations. i.e., Q3 – Q1. This is called inter quartile range. Quartile deviation is the mid point of the range between the two quartiles.
Quartile deviation is define as 
where Q1 and Q3 are the first and the third quartiles respectively.
where Q1 and Q3 are the first and the third quartiles respectively.
PROBLEMS:
1. Calculate the quartile deviation for the following data giving the age distribution of 1500 women. Also find the coefficient of Q.D.
Age in years:
|
16-20
|
20-24
|
24-28
|
28-32
|
32-36
|
36-40
|
No. of women:
|
200
|
250
|
400
|
300
|
250
|
100
|
[ Answer: 4.44 years and 0.16 ]
- Calculate the quartile deviation for the following data.
Sales (’00 Rs.)
|
100-110
|
110-120
|
120-130
|
130-140
|
140-150
|
150-160
|
No. of Shops:
|
4
|
7
|
20
|
9
|
6
|
4
|
[ Answer: 8.24 ]
3. Calculate quartile deviation for the following distribution of ages of 800 persons. Also find the coefficient of quartile deviation.
Age in years:
|
20-25
|
25-30
|
30-35
|
35-40
|
40-45
|
45-50
|
50-55
|
55-60
|
No. of persons:
|
50
|
70
|
100
|
180
|
150
|
120
|
70
|
60
|
[ Answer: 6.54 and 0.1613 ]
4. Find the quartile deviation and the coefficient of Q.D.
C.I.
|
1500-1700
|
1700-1900
|
1900-2100
|
2100-2300
|
2300-2500
|
2500-2700
|
Freq.:
|
70
|
100
|
120
|
150
|
100
|
60
|
[ Answer: 230 and 0.11 ]
5. Find the quartile deviation and the coefficient of Q.D.
Age (less than):
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
No. of persons:
|
15
|
30
|
53
|
75
|
100
|
110
|
115
|
125
|
[ Answer: 13.4783 and 0.3962 ]
6. Find the quartile deviation and the coefficient of Q.D.
Daily wages in Rs.:
|
0-10
|
10-20
|
20-30
|
30-40
|
40-50
|
50-60
|
60-70
|
70-80
|
No. of persons:
|
10
|
17
|
26
|
30
|
33
|
25
|
12
|
9
|
[ Answer: 13.5039 and 0.3489 ]
7. Find the quartile deviation and the coefficient of Q.D.
Marks:
|
5-10
|
10-15
|
15-20
|
20-25
|
25-30
|
30-35
|
35-40
|
Frequency:
|
6
|
8
|
17
|
21
|
15
|
11
|
2
|
[ Answer: 5.451 and 0.2454 ]
8. Find the following data calculate the three quartiles and the quartile deviation and its coefficient.
Age in years:(Less than)
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
No. of persons:
|
14
|
36
|
64
|
99
|
123
|
139
|
149
|
157
|
[ Answer: 13.325 and 0.3864 ]
MEAN DEVIATION
The previous two measures of dispersion viz., Range and Quartile deviation do not take into account, the deviations from the central value. The mean deviation considers these differences in absolute values and averages these differences. Mean deviation takes into account all the observations and therefore is superior to these two measures. Here deviations from mean are calculated considering their absolute values, and are averaged. Although any average can be used theoretically, median is the best to use because mean deviation from the median is less than that from any other value.
Mean Deviation is calculated as follows:
Raw Data
|
Frequency Distribution
|
 |  |
Coefficient of Mean Deviation = 
where 
is mean, median or mode.
where is mean, median or mode.
Problems:
1. Calculate mean deviation from median and the coefficient of M.D for the following distribution of ages of 500 persons.
Age in years:
|
20 – 25
|
25 – 30
|
30 – 35
|
35 – 40
|
40 – 45
|
45 – 50
|
No. of persons:
|
70
|
80
|
180
|
100
|
50
|
20
|
[ Answer: 4.8896 and 0.1492 ]
2. Find the mean deviation from mode and the corresponding coefficient of mean deviation for the following data.
Income in Rs.:
|
800-1000
|
1000-1200
|
1200-1400
|
1400-1600
|
1600-1800
|
No. of persons:
|
16
|
34
|
60
|
37
|
13
|
[ Answer: 163.545 and 0.1252 ]
3. Find the mean deviation from the mean for the following data.
Age in years:
|
11
|
12
|
13
|
14
|
15
|
16
|
No. of students:
|
7
|
19
|
25
|
23
|
15
|
11
|
[ Answer: 1.2 years ]
4. Find the mean deviation from median from the following data.
xi:
|
5
|
6
|
7
|
8
|
9
|
10
|
fi:
|
15
|
20
|
30
|
25
|
12
|
10
|
[ Answer: 1.1518 ]
5. Find the mean, mean deviation and the coefficient of mean deviation from the following data.
Age in years:
|
20-22
|
22-24
|
24-26
|
26-28
|
28-30
|
30-32
|
32-34
|
No. of persons:
|
70
|
90
|
110
|
140
|
130
|
80
|
80
|
[ Answer: 27.09, 2.9582 and 0.1093 ]
6. Find the mean deviation from median for the following data.
Class Interval:
|
10-30
|
30-50
|
50-70
|
70-90
|
90-110
|
110-130
|
130-150
|
Frequency:
|
11
|
18
|
25
|
30
|
14
|
8
|
4
|
[ Answer: Median = 70.67, M.D. = 24.897, Coefficient = 0.3523 ]
7. Calculate Mean Deviation from mean and its corresponding relative measure:
Class Interval:
|
0 – 5
|
5 – 10
|
10 – 15
|
15 – 20
|
20 – 25
|
25 – 30
|
30 – 35
|
Frequency:
|
7
|
14
|
23
|
31
|
28
|
17
|
10
|
[ Mean = 18.26, M.D. = 6.4246, Coefficient = 0.3517 ]
8. Calculate median, mean deviation from median and the coefficient of mean deviation for the following data.
Expenses in Rs.:
|
1000-1300
|
1300-1600
|
1600-1900
|
1900-2200
|
2200-2500
|
No. of Employees:
|
20
|
25
|
35
|
15
|
5
|
[ Answer: 1642.86, 280.71 and 0.1709 ]
9. Find the mode and mean deviation from mode from the following data. Also find the corresponding coefficient of M.D.
Class Interval:
|
0-10
|
10-20
|
20-30
|
30-40
|
40-50
|
50-60
|
60-70
|
Frequency:
|
4
|
7
|
12
|
18
|
8
|
6
|
2
|
[ Answer: 11.4693 and 0.3398 ]
STANDARD DEVIATION
It is the most important and widely used of all the measures of dispersion. In mean deviation algebraic signs are ignored. In standard deviation, the deviations are squared to get positive values. Here the deviations from arithmetic mean are squared, they are averaged and the squareroot of the resulting quantity is taken. Therefore this is also known as ‘root-mean square deviation’.
If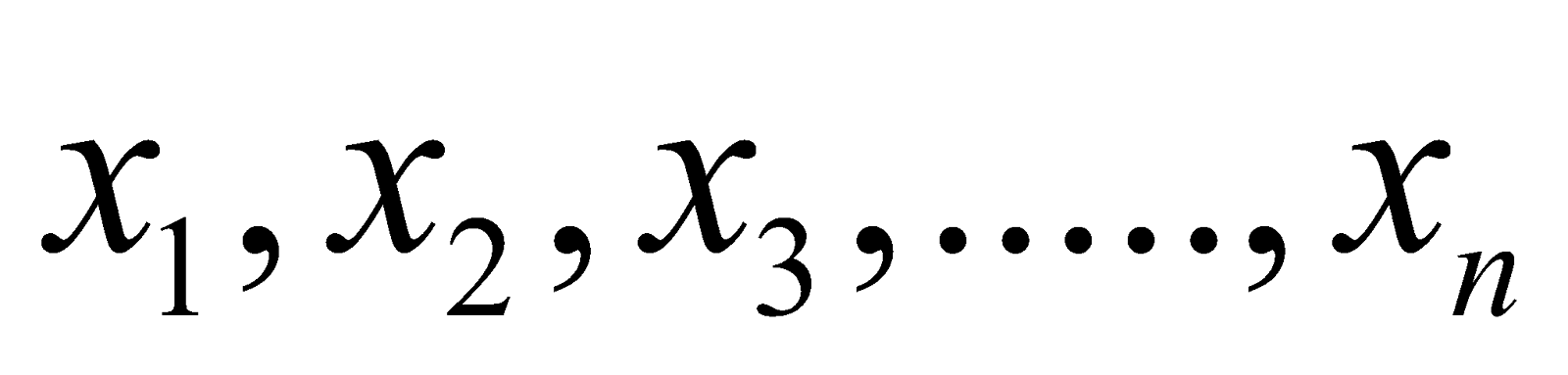 
are n observations then their standard deviation denoted by ‘
’ is given
are n observations then their standard deviation denoted by ‘’ is given
by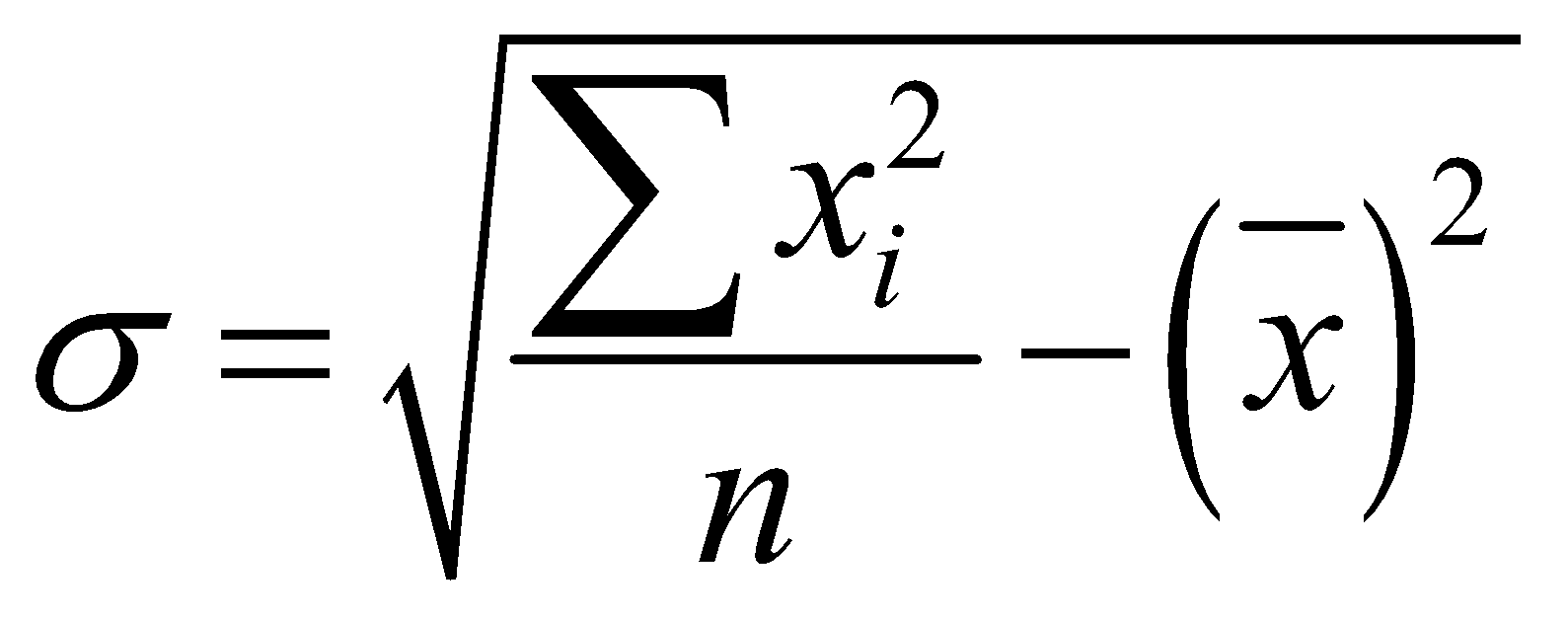 
or 
or
In the case of a frequency distribution the standard deviation is calculated as follows:
The corresponding relative measure known as the coefficient of variation is calculated as
Problems:
- Find the standard deviation for the following sets of values:
- 15, 20, 17, 8, 9, 12, 18, 10
- 652, 672, 670, 639, 642, 670
- 85, 35, 43, 75, 42, 41
- 52, 57, 49, 48, 35, 37
[ Answer: i. 4.2112 ii. 13.7568 iii. 19.1289 iv. 7.867 ]
2. From the following distribution, find the standard deviation.
i.
|
xi:
|
11
|
12
|
13
|
14
|
15
|
16
|
17
| |||||||
fi:
|
3
|
6
|
10
|
8
|
5
|
3
|
2
| ||||||||
ii.
|
xi:
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
| ||||||
fi:
|
5
|
8
|
12
|
9
|
7
|
5
|
2
|
1
| |||||||
[ Answer: i. 1.5657 ii. 17.189 ]
3. From the following data, calculate the Coefficient of variation..
Marks:
|
0-5
|
5-10
|
10-15
|
15-20
|
20-25
|
25-30
|
30-35
|
35-40
|
No. of students:
|
2
|
5
|
7
|
13
|
21
|
16
|
8
|
3
|
[ Answer: 36.52% ]
4. Find the mean, standard deviation and coefficient of variation.
Age in years:
|
0-10
|
10-20
|
20-30
|
30-40
|
40-50
|
50-60
|
No. of persons:
|
3
|
7
|
12
|
10
|
4
|
2
|
[ Answer: 27.89, 12.546, 44.9839% ]
5. Find the standard deviation:
Marks:
|
5-15
|
15-25
|
25-35
|
35-45
|
45-55
|
55-65
|
No. of students:
|
7
|
12
|
20
|
14
|
8
|
2
|
[ Answer: 12.75 ]
6. The daily wages of 69 workers are given below. Find the standard deviation of wages:
Daily wages in Rs.:
|
30-40
|
40-50
|
50-60
|
60-70
|
70-80
|
80-90
|
No. of workers:
|
7
|
13
|
21
|
15
|
8
|
5
|
[ Answer: Rs. 13.61 ]
7. Find the standard deviation of the following data. Also find the coefficient of variation.
Class Interval:
|
20-40
|
40-60
|
60-80
|
80-100
|
100-120
|
120-140
|
Frequency:
|
7
|
12
|
16
|
13
|
13
|
4
|
[ Answer: 28.4345 and 36.5988% ]
8. Find the standard deviation and the coefficient of variation for the following data:
Daily collection in Rs.
|
2500-3000
|
3000-3500
|
3500-4000
|
4000-4500
|
4500-5000
|
No. of Agents:
|
11
|
15
|
18
|
14
|
8
|
[ Answer: 628.4106 and 16.99% ]
9. The following data gives returns, expressed in percentages, from two types of investments A and B over a period of 7 years. Which type gives a more consistent return?
Type A
|
18
|
13
|
9
|
21
|
20
|
12
|
25
|
Type B
|
15
|
22
|
27
|
11
|
9
|
21
|
14
|
[ Answer: Type A is more consistent ]
10. Find in which of the following subjects, there is more variation of marks.
Subject A:
|
57
|
27
|
61
|
39
|
7
|
95
|
80
|
16
|
5
|
56
|
Subject B:
|
21
|
16
|
78
|
70
|
41
|
43
|
57
|
35
|
14
|
22
|
[ Answer: (C.V.)A = 65.76, (C.V.)B = 54.05. Subject A is more variable ]
11. Find the coefficients of variation for the following sets representing marks of two groups of students. Which group is more consistent?
Group A:
|
85
|
83
|
87
|
90
|
65
|
75
|
57
|
70
|
Group B:
|
84
|
83
|
72
|
79
|
75
|
70
|
67
|
80
|
[ Answer: (C.V.)A = 14.3494, (C.V.)B = 7.6401, Group B is more consistent ]
12. The mean and standard deviation of a group of observation are 25.5 and 10.87 respectively. For another group of observations of the same type, the mean and standard deviation are 37.5 and 4.89. Which group is more variable?
[ Answer: Group I is more variable ]
13. The mean and standard deviation of a group of observations are 25.5 and 10.87 respectively. For another group of observations of the same type the mean and standard deviation are 37.5 and 4.89 respectively. Which group is more consistent?
[ Answer: Group I is more variable ]
14. The following is the data representing profits in thousands of rupees of some companies. Find the coefficient of variation.
Profit (‘000 Rs)
|
20-40
|
40-60
|
60-80
|
80-100
|
100-120
|
120-140
|
No. of companies:
|
7
|
12
|
16
|
13
|
13
|
4
|
[ Answer: 16.3486% ]
15. The distribution of payments to a number of salesmen is given below. Find the standard deviation and coefficient of variation.
Payment in Rs.:
|
No. of Salesmen
|
Payment in Rs.:
|
No. of Salesmen
| |
100 – 120
|
4
|
200 – 220
|
50
| |
120 – 140
|
10
|
220 – 240
|
32
| |
140 – 160
|
16
|
240 – 260
|
23
| |
160 – 180
|
29
|
260 – 280
|
17
| |
180 – 200
|
52
|
280 – 300
|
7
|
[ Answer: 19.3721% ]
16. Find the coefficient of variation for the following data:
Amount in Rs.
|
No. of workers
|
Amount in Rs.
|
No. of workers
| |
500 – 599
|
25
|
900 – 999
|
62
| |
600 – 699
|
42
|
1000 – 1099
|
50
| |
700 – 799
|
55
|
1100 – 1199
|
35
| |
800 – 899
|
70
|
1200 – 1299
|
11
|
[ Answer: 20.8793% ]
Combined Standard Deviation:
If n1 and n2 are the number of observations of two groups with means 
and 
and standard deviations 
and 
respectively then their combined standard deviation denoted by 
is given by
and and standard deviations and respectively then their combined standard deviation denoted by 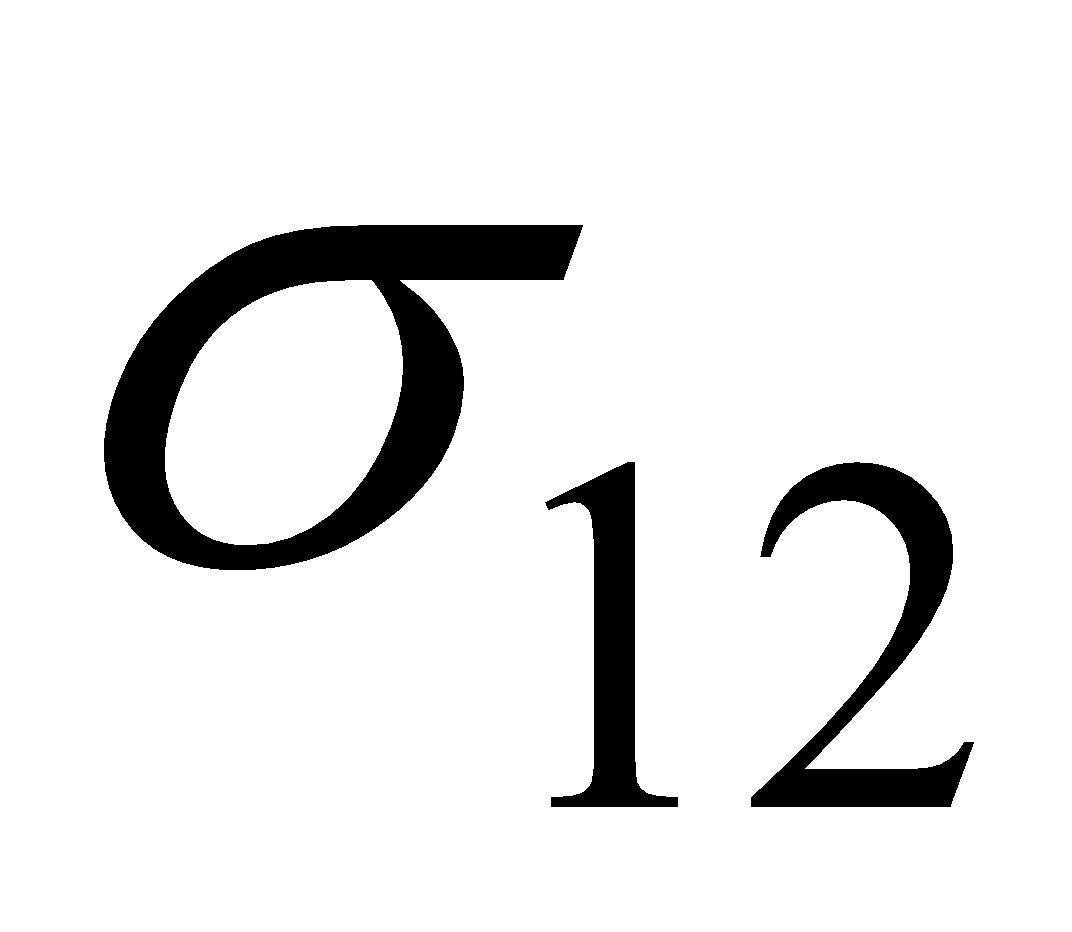is given by =
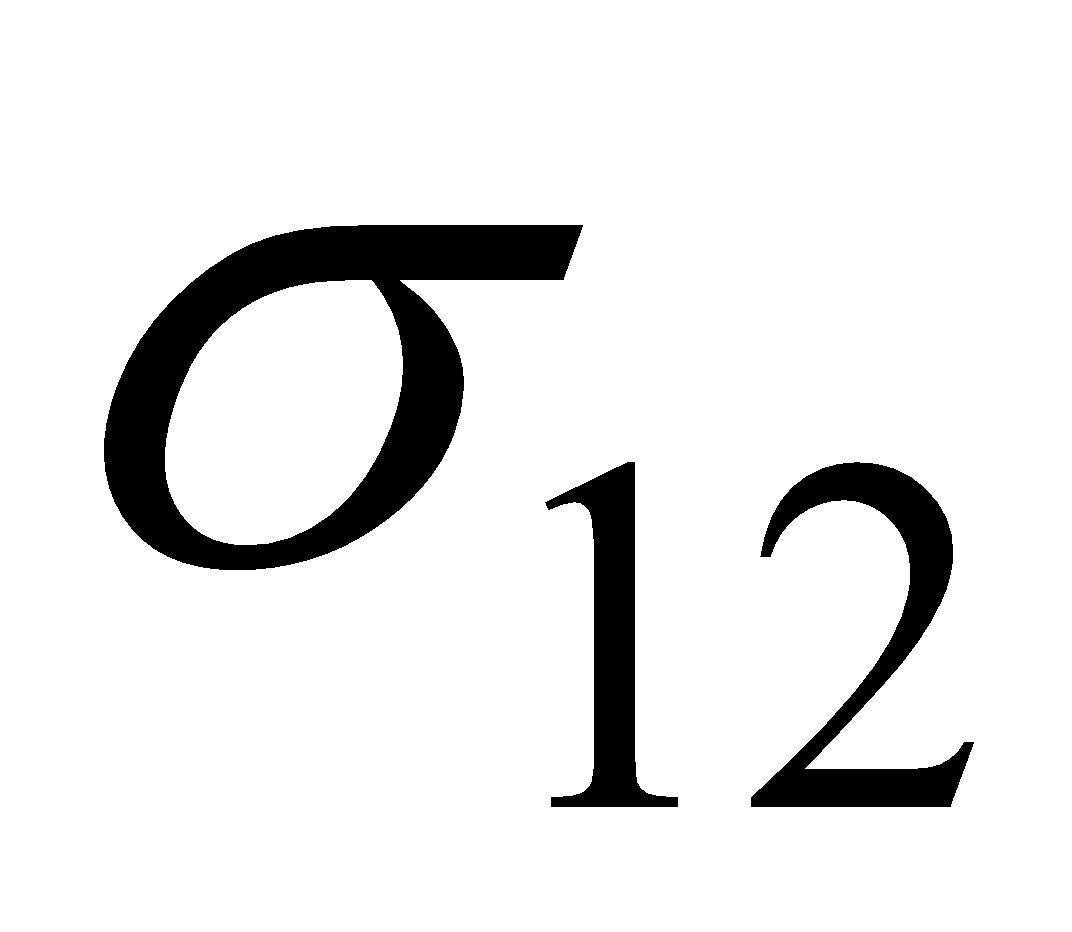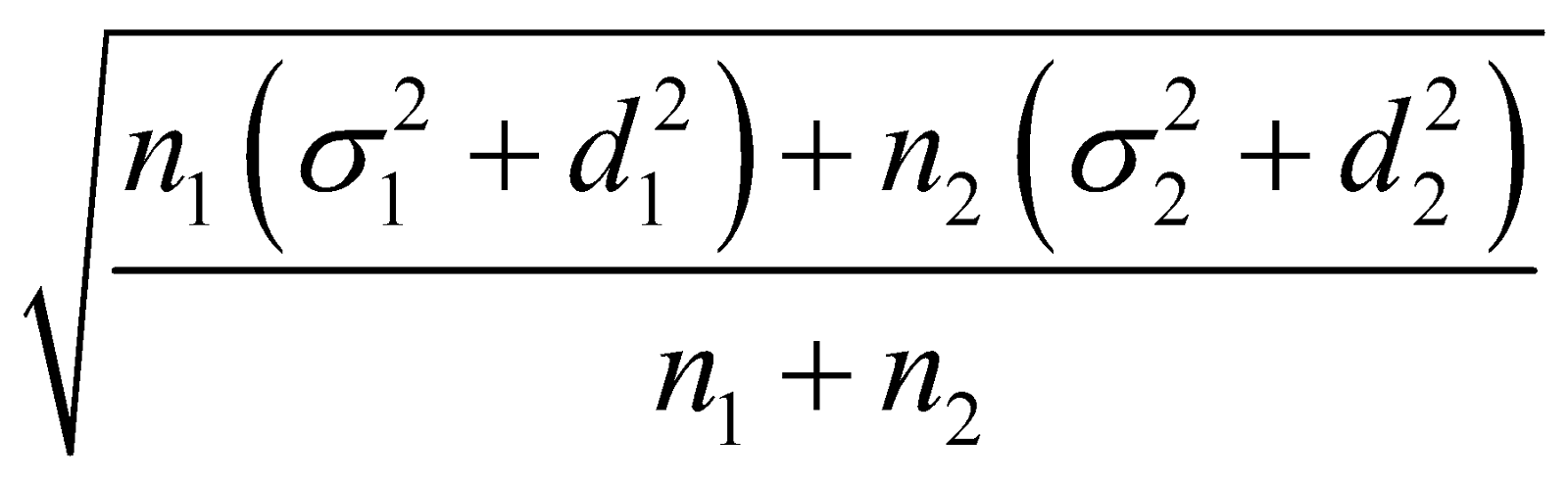
Where 
Problems:
1. The following are some particulars of the distribution of weights of boys and girls in a class. Find the standard deviation of the combined group.
Boys
|
Girls
| |
Number
|
100
|
50
|
Mean weight
|
60 kgs.
|
45 kgs.
|
Std. Deviation
|
3 kgs.
|
2 kgs.
|
[ Answer: 7.57 kgs. ]
2. Find the combined mean and combined standard deviation for the following:
Male
|
Female
| |
Number
|
40
|
60
|
Mean Height
|
170 cms
|
160 cms
|
Std. Deviation
|
5 cms.
|
2 cms
|
[ Answer: 164 cms & 6.03 cms ]
3 Find the combined mean and combined standard deviation for the following:
Group I
|
Group II
| |
Number
|
70
|
90
|
Mean Height
|
75
|
82
|
Std. Deviation
|
4
|
7
|
[ Answer: 78.9375 & 6.83 ]
4. The first of the two samples in a group has 100 items with mean 15 and standard deviation 3. If the whole group has 250 items with mean 15.6 and standard deviation 
, find the standard deviation of the second group. [ Answer: 4 ]
, find the standard deviation of the second group. [ Answer: 4 ]
5. There are two groups of workers with the following information:
Group I
|
Group II
| |
Number
|
400
|
500
|
Mean Height
|
Rs.50
|
Rs.41
|
Std. Deviation
|
Rs.5
|
…
|
The standard deviation of the combined group of 900 workers is Rs.
. Find the standard deviation of the second group. [ Answer: 3.2557 ]
. Find the standard deviation of the second group. [ Answer: 3.2557 ]
6. Find the combined mean and combined standard deviation for the following:
Group I
|
Group II
| |
Number
|
50
|
150
|
Mean Height
|
240
|
220
|
Variance
|
196
|
324
|
[ Answer: 225 & 19.1572 ]
7. Find the combined mean and combined standard deviation for the following:
Group I
|
Group II
| |
Number
|
100
|
200
|
Mean Height
|
83
|
87
|
Variance
|
16
|
9
|
[ Answer: 11.9 ]
8. The arithmetic mean and the standard deviation of 100 items are found to be 40 and 10 respectively. If at the time of calculations one item was wrongly taken as 30 instead of 3. Find the correct mean and correct standard deviation. [ Answer: 39.73 & 10.6121 ]
9. The arithmetic mean and standard deviation of a group of 200 items were 150 and 19 respectively. It was afterwards found that one item was wrongly considered as 155 instead of 125. Find the correct mean and correct standard deviation.
[ Answer: 149.85 & 19.0782 ]
10. The values of mean and standard deviation for 50 observations were 475 and 25 respectively. It was observed that one item was wrongly considered as 400 instead of 500. Find the correct mean and correct standard deviation.
[ Answer: 477 & 22.8254 ]
11. The mean and standard deviation of a group of 30 observations were respectively 125 and 11. It was afterwards found that two observations were wrongly considered as 105 and 107 instead of 135 and 137 respectively. Find the correct mean and correct standard deviation.
[ Answer: 127 and 10.049 ]
12. The mean and standard deviation of 25 observations were 42 and 8 respectively. Two values were wrongly recorded as 25 and 20. Find the correct mean and correct standard deviation after deleting the wrong values.
[ Answer: 43.6957 & 5.7513 ]
13. The mean and standard deviation of a group of 30 observations were 93 and 7 respectively. It was detected that three observations were wrongly taken as 89, 65 and 73. Find the correct mean and correct standard deviation after deleting the wrong values.
[ Answer: 94.106 & 5.044 ]
14. The arithmetic mean and standard deviation of the wage distribution of 1000 workers are Rs.480/- and Rs.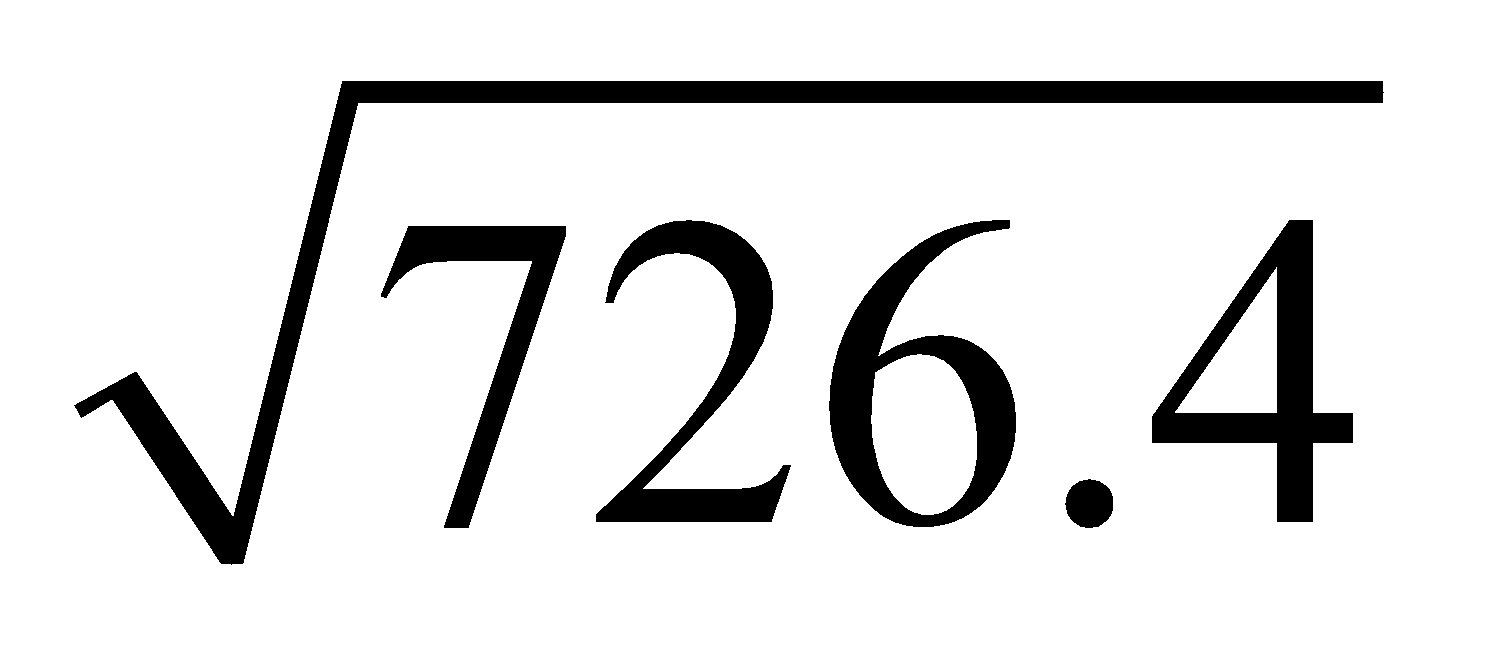
. The arithmetic mean and standard deviation of 400 workers out of them are Rs.450/- and Rs.10/-. Find the mean and standard deviation of the remaining 600 workers.
. The arithmetic mean and standard deviation of 400 workers out of them are Rs.450/- and Rs.10/-. Find the mean and standard deviation of the remaining 600 workers.
[ Answer: Rs.500/- and Rs.12/- ]
- The coefficient of variation of a group of observations was 23.0716% and the mean was 57.2 Find the standard deviation of the group.
[ Answer: 13.1970 ]
16. The coefficient of variation for a group was 30.908 and mean is 13.625. Find the standard deviation.
[ Answer: 4.2112 ]
17. The standard deviation and coefficient of variation of a distribution are 13.7568 and 2.0923. Find the mean.
[ Answer: 657.4965 ]
18. The following data gives the means and standard deviations of two groups of workers.
Group A
|
Group B
| |
Number
|
400
|
600
|
Mean Height
|
Rs.450/-
|
Rs.500/-
|
Variance
|
Rs.10/-
|
Rs.12/-
|
Find i) Which group has a larger wage bill?
ii) Which group is more consistent?
iii) What is the combined mean and standard deviation of all the workers taken together?
[ Answer: i. Group B ii. Group A iii. 480 and 29.951 ]
