Regression analysis is a method of predicting or estimating one variable knowing the value of the other variable. Estimation is required in different fields in every day life. A businessman wants to know the effect of increase in advertising expenditure on sales or a doctor wishes to observe the effect of a new drug on patients. An economist is interested in finding the effect of change in demand pattern of some commodities on prices.
We observe, different pairs of variables related to each other like saving depends upon income, cost of production depends upon the number of units produced, the production depends on the number of workers present on a particular day etc. The relationship between two variables can be established with the help of any measure of correlation, as we have seen in the previous chapter. When it is observed that two variables are highly correlated, it leads to interdependence of the variables. We can study the cause and effect relationship between them and then we can apply the regression analysis. The analysis helps in finding a mathematical model of the relationship. In this chapter we will discuss linear regression only.
There are two types of regression lines viz., regression equation of x on y and regression equation of y on x. The first one is used to estimate the value of x when the corresponding value of y is given and the second used to find the value of y when the corresponding value of x is given. They are given by
Regression equation of x on y is 
and
and
Regression equation of y on x is 
where 
and 
are known as regression coefficients.
where and are known as regression coefficients.
The regression coefficients are given by
Thus, when the regression coefficients are known to us we can determine the co-efficient of correlation.
The regression coefficients can be found independently as
Problems:
- From the following data find the two regression equations and hence estimate y when x = 13 and estimate x when y = 10.
x:
|
14
|
10
|
15
|
11
|
9
|
12
|
6
|
y:
|
8
|
6
|
4
|
3
|
7
|
5
|
9
|
[ Answer: 5.2858 & 8.1428 ]
2. Find the two regression equations and also estimate y when x = 13 and estimate x when y = 10
x:
|
11
|
7
|
9
|
5
|
8
|
6
|
10
|
y:
|
16
|
14
|
12
|
11
|
15
|
14
|
17
|
[ Answer: 17.5359 & 5.0693 ]
3. The following data represents the marks in Algebra (x) and Geometry (y) of a group of 10 students. Find both regression equations and hence estimate y if x = 78 and x if y = 94.
x:
|
75
|
80
|
93
|
65
|
87
|
71
|
98
|
68
|
89
|
77
|
y:
|
82
|
78
|
86
|
72
|
91
|
80
|
95
|
72
|
89
|
74
|
[ Answer: 80.394 ~ 80 and 94.9337 ~ 95 ]
4. Find the regression equations for the following data and hence estimate y when x = 15 and x when y = 18.
x:
|
10
|
12
|
14
|
19
|
8
|
11
|
17
|
y:
|
20
|
24
|
25
|
21
|
16
|
22
|
20
|
[ Answer: 21.64 & 11.54 ]
5. From the following data, find the regression equations and further estimate y if x = 16 and x if y = 18.
x:
|
3
|
4
|
6
|
10
|
12
|
13
|
y:
|
12
|
11
|
15
|
16
|
19
|
17
|
[ Answer: 20.32 & 11.8 ]
6. The heights in cms of a group of mothers and daughters are given below. Find the regression equations and hence find the most likely height of a mother when the daughter’s height is 164 cms. Also obtain the estimate of the height of a daughter when mother’s height is 162 cms.
Height of mother (x):
|
157
|
160
|
163
|
165
|
167
|
168
|
170
|
164
|
Height of daughter (y):
|
162
|
159
|
165
|
167
|
172
|
170
|
168
|
166
|
[ Answer: 164.2942 & 162.4556 ]
7. The following data gives the marks obtained at the preliminary examination (x) and the final examination (y) for a group of 10 students. Obtain the regression equation of y on x. Hence find the most probable marks at the final examination of a student who has scored 70 marks at the preliminary examination.
x:
|
54
|
65
|
75
|
82
|
57
|
59
|
60
|
64
|
58
|
62
|
y:
|
58
|
67
|
76
|
80
|
60
|
64
|
65
|
65
|
60
|
70
|
[ Answer: 71.21 ]
8. The following data gives the expenditure on advertising, expressed in hundreds of Rs. (x) and the expenditure on office staff, expressed in thousands of Rs. (y) for 7 different companies. Find the two regression equations and hence estimate the expenditure on advertising when expenditure on office staff is Rs.97,000. Also obtain the most likely expenditure on office staff when the advertising expenditure is Rs.13,200.
x:
|
129
|
137
|
138
|
135
|
139
|
134
|
145
|
y:
|
98
|
94
|
93
|
91
|
96
|
95
|
100
|
[ Answer: Rs.13746 and Rs.94780 ]
9. The following data represents the figures in kgs. for demands of two commodities A and B. Find (i) the most probable demand for A when demand for B is 107 kgs. (ii) the most probable demand for B when demand for A is 115 kgs.
x:
|
107
|
113
|
109
|
103
|
110
|
117
|
114
|
y:
|
105
|
110
|
103
|
100
|
110
|
111
|
108
|
[ Answer: 110.7069 & 110.0996 ]
10. From the following data, estimate y when x = 142 and x when y = 126.
x:
|
140
|
155
|
163
|
167
|
145
|
150
|
148
|
y:
|
122
|
135
|
140
|
139
|
125
|
130
|
125
|
[ Answer: 123.25 & 146.3 ]
11. For a bivariate distribution, the following results are obtained.
Mean value of x = 65
|
Mean value of y = 53
|
Standard deviation = 4.7
|
Standard deviation = 5.2
|
Coefficient of correlation = 0.78
| |
Find the two regression equations and hence obtain
- The most probable value of y when x = 63
- The most probable value of x when y = 50
[ Answer: 51.274 & 62.885 ]
12. Given that for 10 pair of observations.
Find the regression equation of y on x and then estimate y when x = 78.
[ Answer: 81.4495 ]
13. The averages for rainfall and yield of a crop are 42.7 cms and 850 kgs respectively. The corresponding standard deviations are 3.2 cms and 14.1 kgs. The coefficient of correlation is 0.65. Estimate the yield when the rainfall is 39.2 cms. [ Estimated yield is 839.99 kgs. ]
14. The regression equation of supply in thousands of Rs.(y) on price in thousands of Rs.(x) is 
. The average supply is Rs.18,000. The ratio of standard deviation of supply and price is 
. Find the average price and the coefficient of correlation between supply and price. [ Average price is Rs.15,000 & r = 0.6 ]
. The average supply is Rs.18,000. The ratio of standard deviation of supply and price is . Find the average price and the coefficient of correlation between supply and price. [ Average price is Rs.15,000 & r = 0.6 ]
15. Find the regression equation and hence estimate y when x = 56 and x when y = 45.
[ 40.9 & 62.04 ]
16. Given the two regression equations, find
(i) mean values of x and y
(ii) coefficient of correlation
where the equation are 
[ 1, 1 and 0.9682 ]
17. Given the regression equations
. Find the means of x and y and the coefficient of correlation. [1, 1 and -0.8165 ]
18. Find the mean values of x and y and correlation coefficient, if the regression equations are 
[ 1, 1 and -0.5774 ]
[ 1, 1 and -0.5774 ]
19. Given the regression equations 
, find
, find- Mean values of x and y
- Coefficient of correlation
- Estimate of y when x = 17
- Estimate of x when y = 25
[ 15, 20, 0.4714, 21.33 and 16.67 ]
20. Find the two regression equations for the following:
[ 
]
]
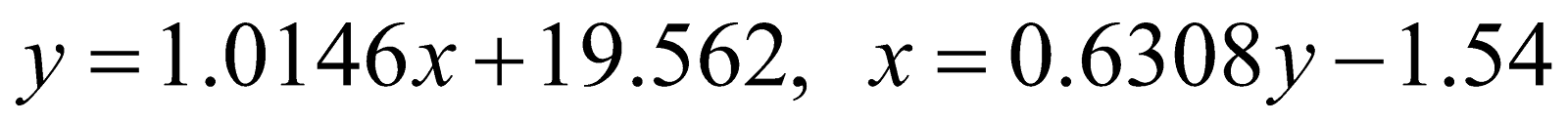21. The regression equation of income (x) on expenditure (y) is 
. The ratio of the standard deviation of income and expenditure is 4 : 3. Find the coefficient of correlation between income and expenditure. Also find the average income if the average expenditure is Rs.1800. [2500, 0.5 ]
. The ratio of the standard deviation of income and expenditure is 4 : 3. Find the coefficient of correlation between income and expenditure. Also find the average income if the average expenditure is Rs.1800. [2500, 0.5 ]
22. From the following regression equations 
, find
, find- Mean values of x and y
- Coefficient of correlation
- Most probable value of y when x = 28
- Most probable value of x when y = 35. [ 25, 33, 0.8164, 37, 26 ]
