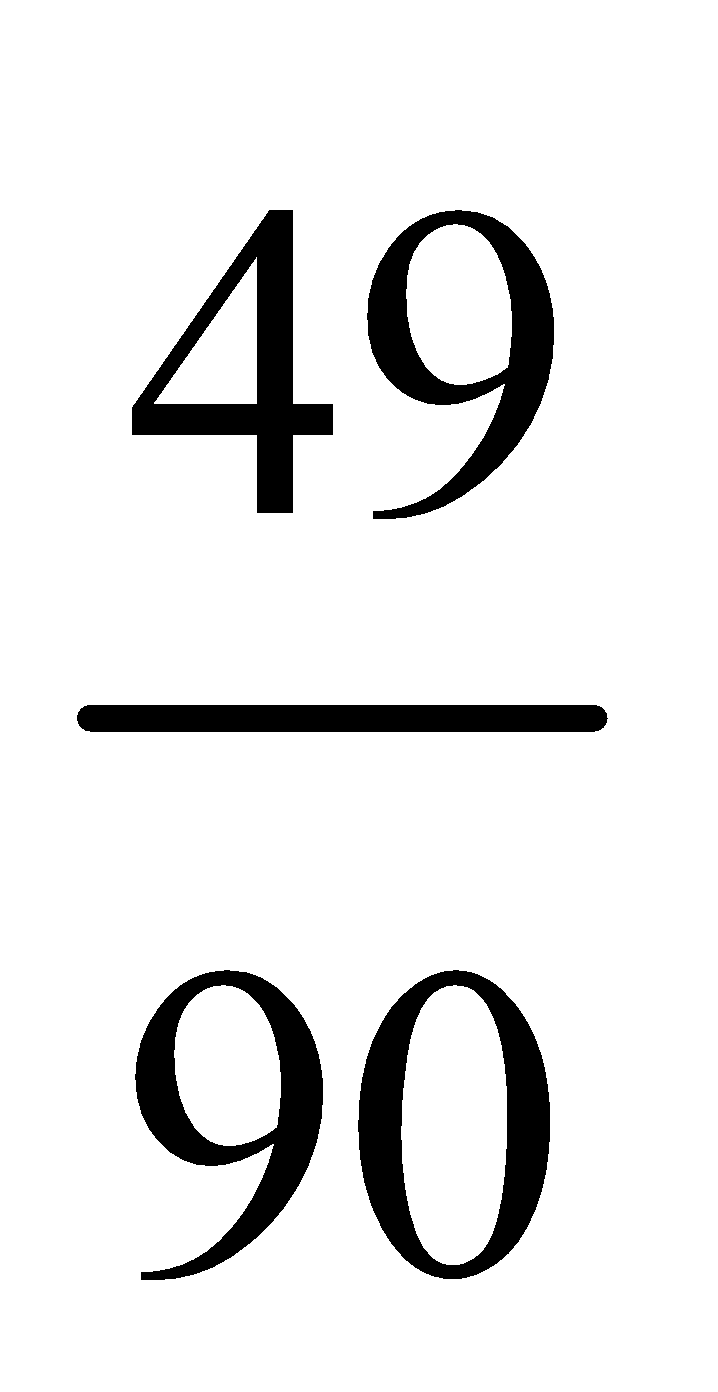Chapter : 7 PROBABILITY
1. A card is drawn from a full well shuffled pack of cards. Find the probability that the card drawn is a king. 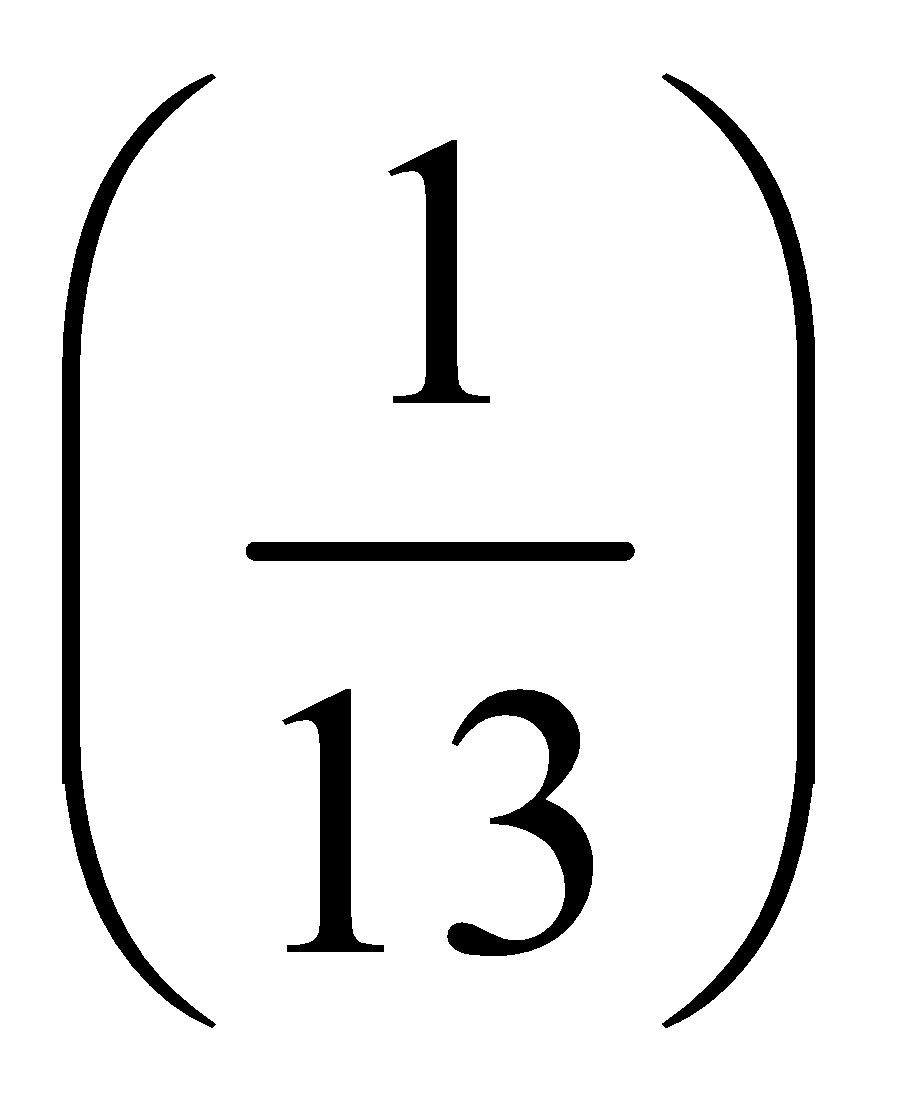
2. If three cards are drawn at random from a pack of 52 cards, what is the probability that all the three will be kings? 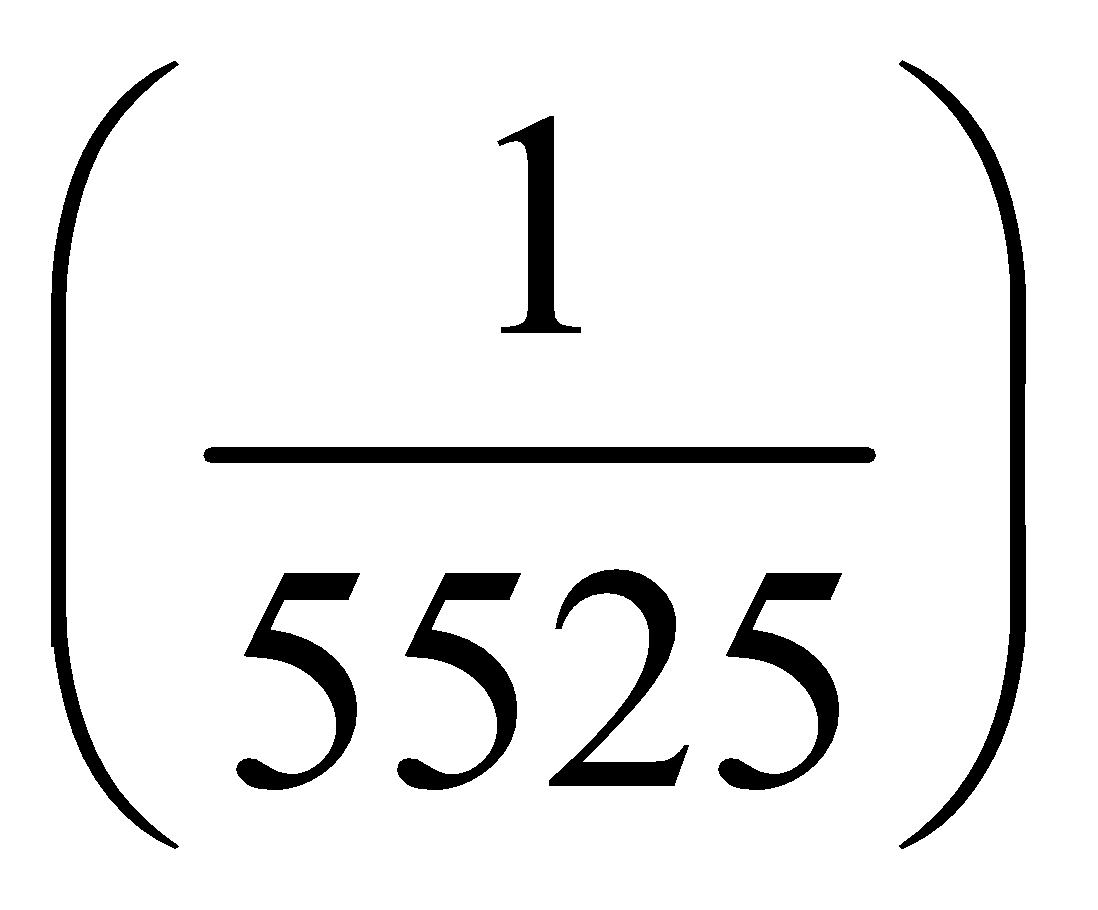
3. Find the probability that the number 3 or 4 turn up in a single toss of a die. 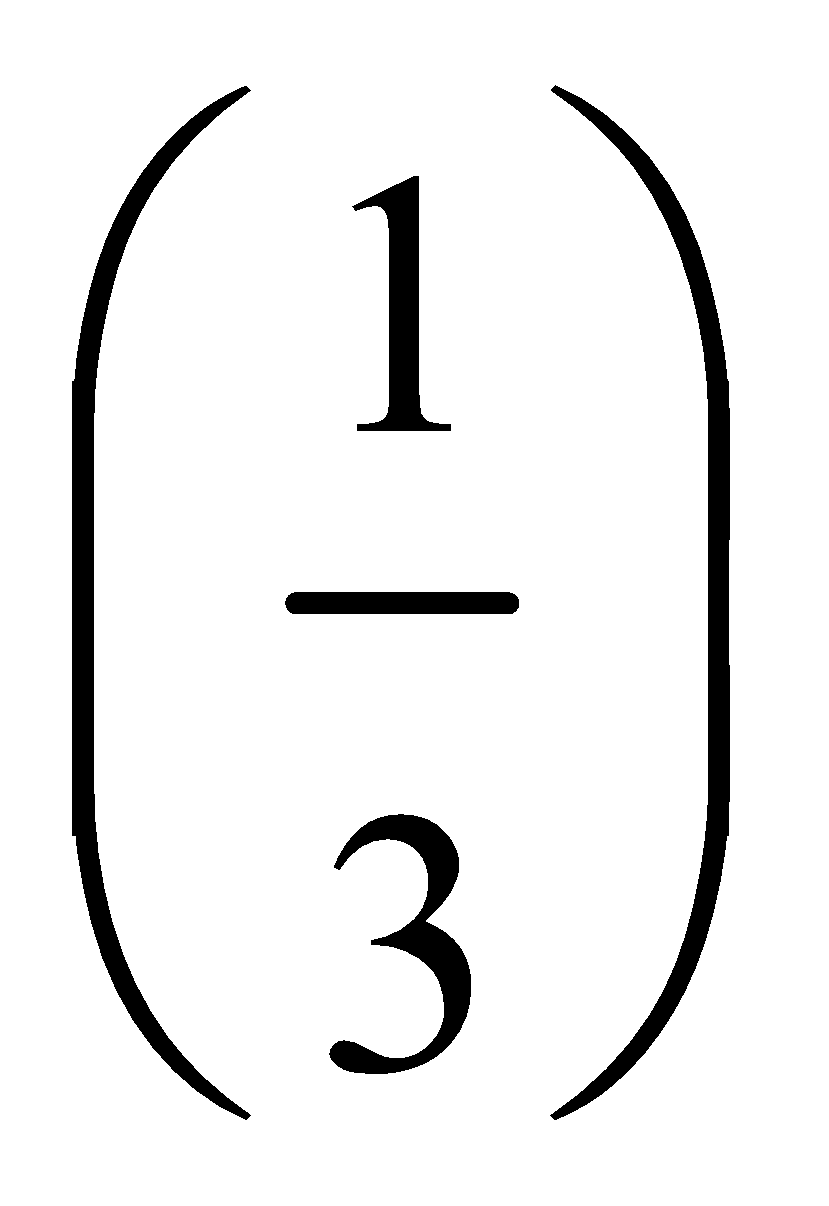
4. Find the probability that at least one head appears in two tosses of a coin. 
5. A box contains 8 red and 3 white balls. If 3 balls are drawn at random, find the probability that (i) all the three are red; (ii) all the three are white; (iii) 2 are red and 1 is white. 
6. A box contains 3 white balls, 4 black balls and 5 red balls. If 3 balls are drawn at random find the probability that (i) all 3 are red; (ii) all 3 are black; (iii) 2 are red and 1 is black; (iv) 1 of each colour. 
7. If four coins are tossed, find the probability of the occurrence of 2 heads and 2 tails. 
8. Two dice are cast simultaneously. Find the probability that i) sum of the numbers on the uppermost faces is 7 ii) the sum is less than or equal to 5 iii) the sum is 7 or 11. 
9. Five cards are drawn from a pack of 52 well shuffled cards. Find the probability that (i) 4 are aces; (ii) 4 are aces and 1 is a king; (iii) 3 are tens and 2 are jacks; (iv) at least one face card is obtained. 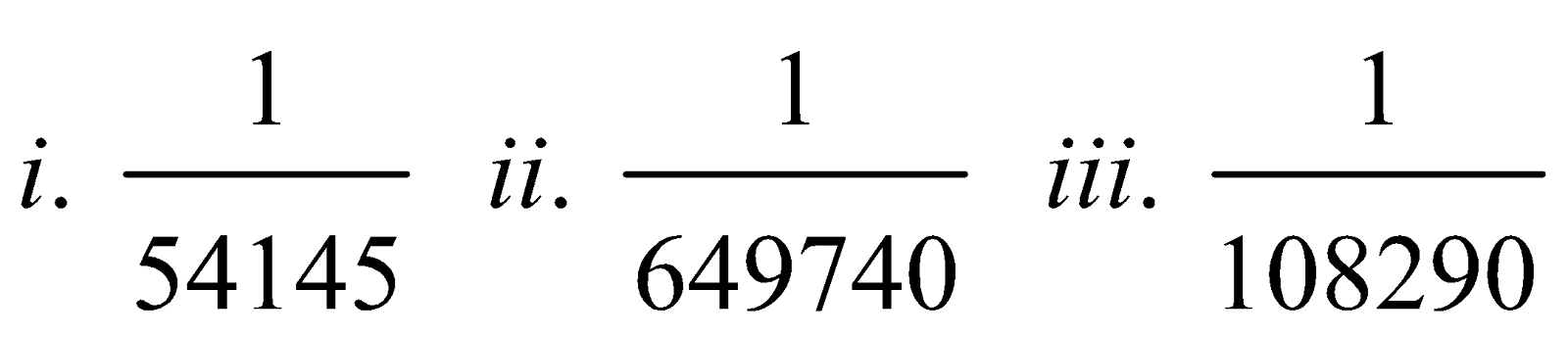
10. A committee of 4 boys and 3 girls is to be formed by lots from 8 boys and 5 girls. One of the boys is a brother of one of the girls. Find the probability that both are included in the committee. 
11. Three groups of children contain (i) 3 girls and 1 boy (ii) 3 girls and 3 boys (iii) 2 boys and 1 girl. One child is selected at random from each group. Find the probability that the three selected children comprise of 1 girl and 2 boys. 
12. A card is drawn at random from a full pack of cards. Find the probability that the card is not a face card (i.e., a king, queen or jack)  .
.
13. Five coins are tossed simultaneously. Find the probability that at least one of them gives a head. 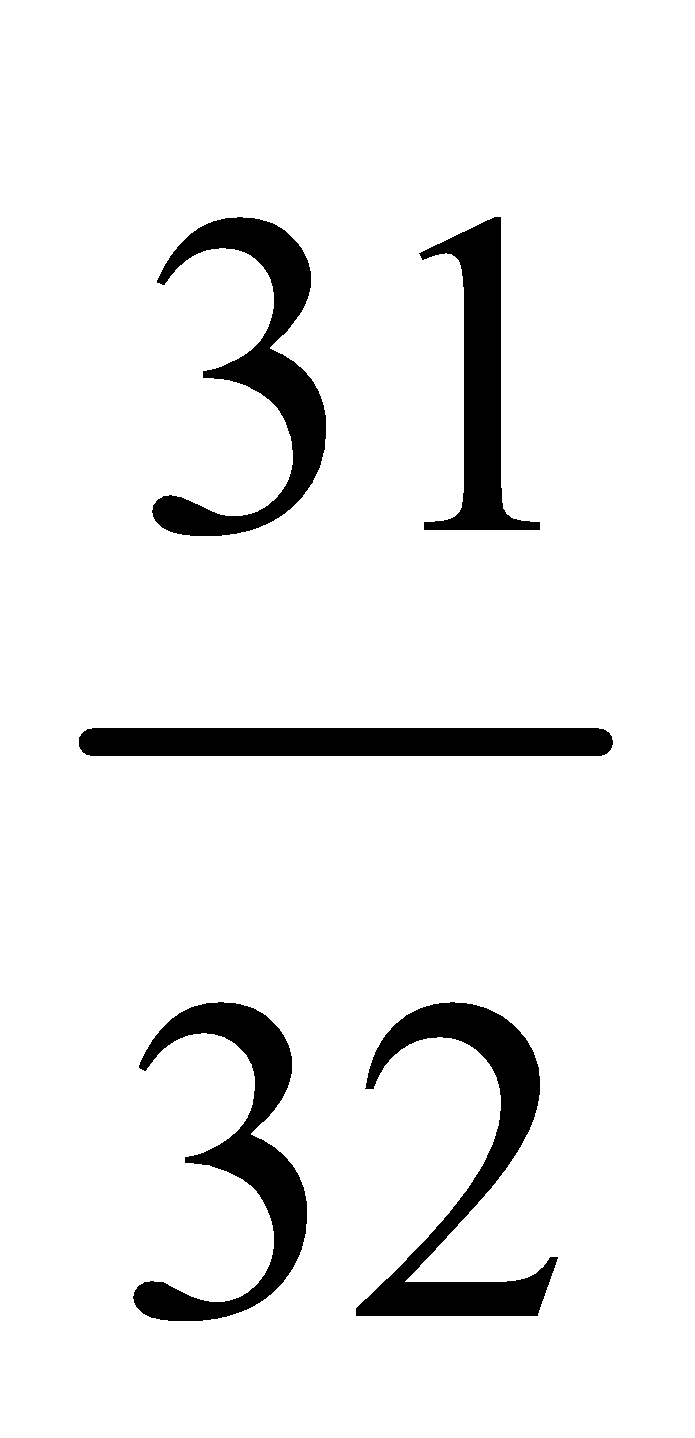
14. A room has three sockets for bulbs. From a collection of 10 light bulbs of which 6 are defective, a person selects 3 at random and puts them in the sockets. What is the probability that at least one bulb gives light? 
15. Find the probability of getting the sum 7 or 10 on the uppermost faces when a pair of dice is thrown.  .
.
16. Two dice are thrown. Find the probability that the sum of the numbers on the uppermost faces is either even or a perfect square. 
17. A bag contains 6 red, 15 blue, 3 white and 4 black balls. A ball is drawn at random. Find the probability that the ball drawn is red, blue or black. 
18. A card is taken from a pack of 52 well shuffled cards. What is the probability that the card drawn is a spade or a face card? 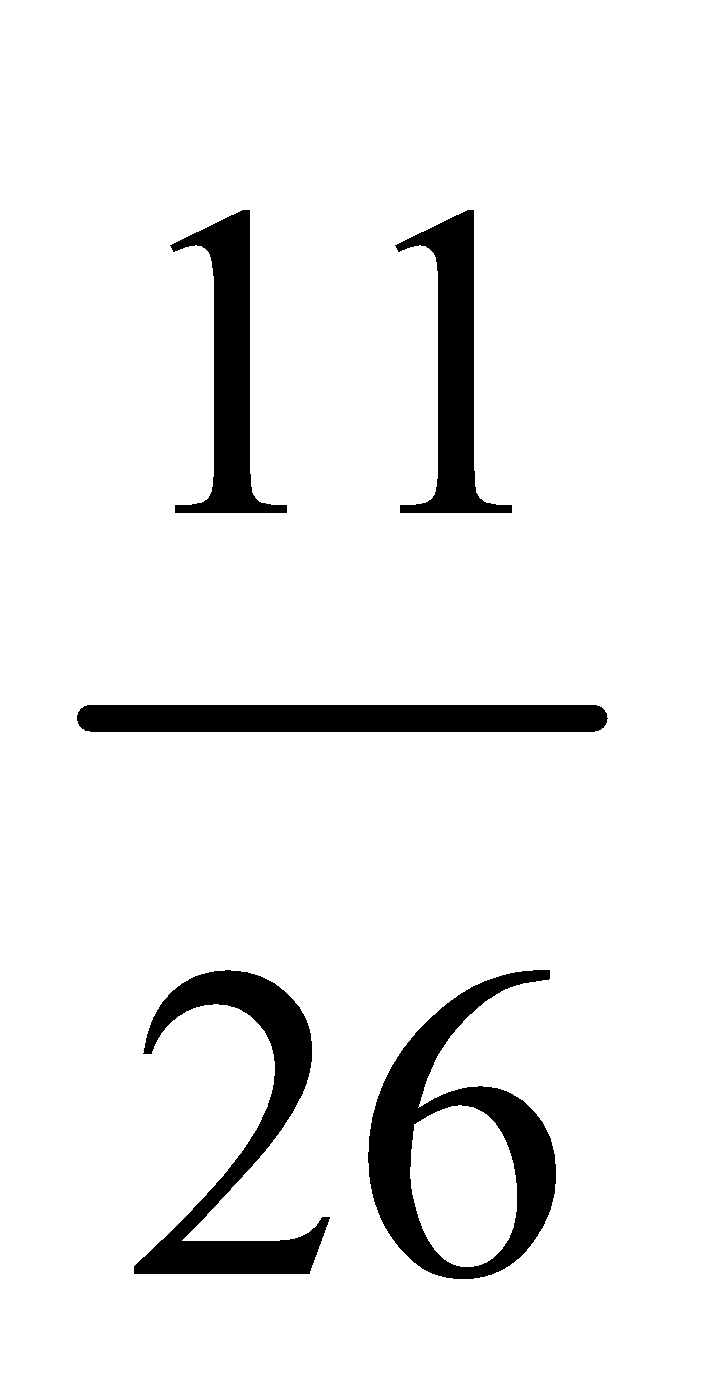
19. One ticket is drawn at random from a lot of 20 tickets numbered from 1 to 20. What is the probability that the number on the ticket drawn is divisible by (i) 2 or 3 (ii) 3 or 7? 
20. A card is drawn from an ordinary deck of 52 well shuffled cards. Find the probability that it is (i) neither red nor an ace; (ii) neither the ten of clubs nor an ace. 
21. In a class of 100 students, 60 drink tea, 50 drink coffee and 30 drink both tea and coffee. A student from this class is selected at random. What is the probability that the selected student takes (i) at least one of the two drinks, (ii) only one of the drinks? 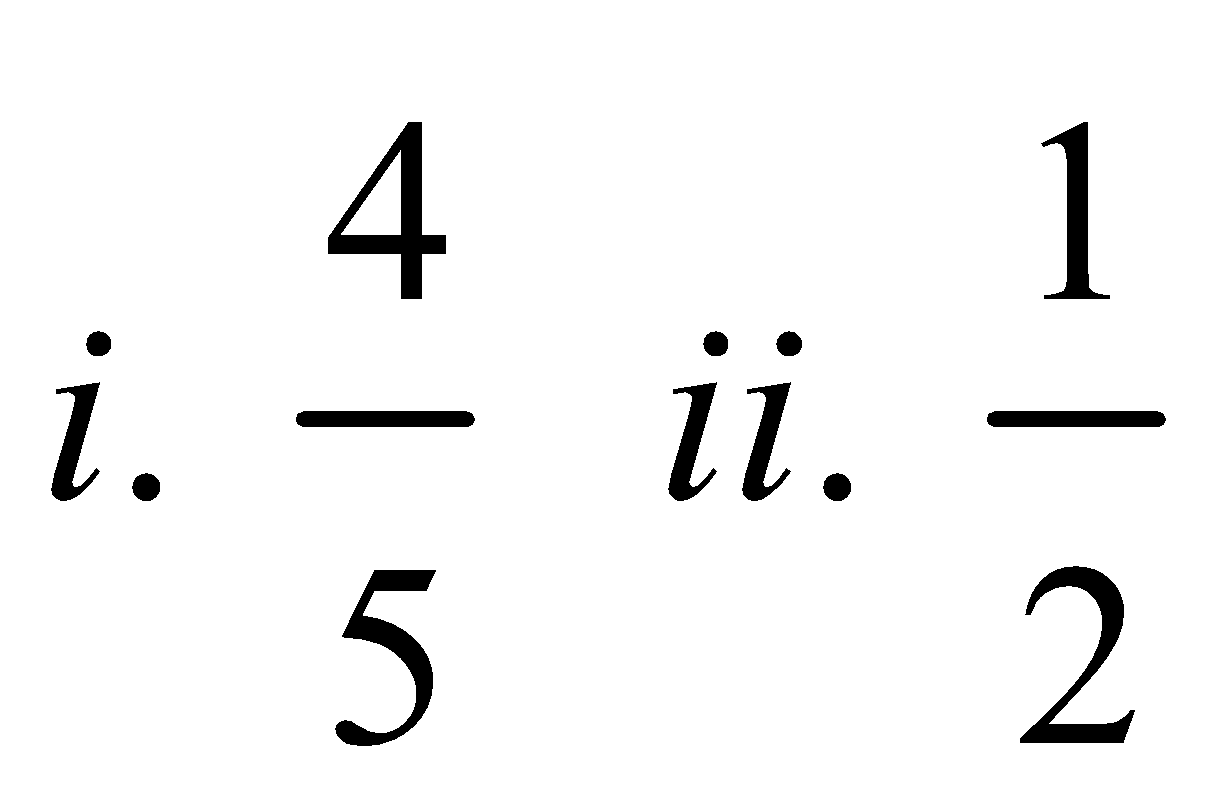
22. A marble is drawn at random from a box containing 10 red, 30 white, 20 blue and 15 orange marbles. Find the probability that it is (i) red or orange, (ii) neither red nor blue (iii) not blue, (iv) white, (v) red, white or blue. 
23. Out of 80 students in a class, 30 passed in Mathematics, 20 passed in Statistics and 10 passed in both. One student is selected at random. Find the probability that he has passed in (i) at least one of the subjects (ii) none of the subjects (iii) only in Mathematics (iv) only in Mathematics or only in Statistics. 
24. A die is thrown twice. Find the probability that the score in the first throw is 6 and the score in the second throw is 5 or 6. 
25. Two cards are drawn from a full pack, the first card being returned to the pack before the second is taken. What is the probability that both the extracted cards are aces? 
26. Suppose two dice are cast. Find the probability that the number on the uppermost face of the first die is even and that of the second is odd. 
27. Two cards are drawn from a well shuffled deck of 52 cards. Find the probability that they are both aces if the first card is (i) replaced, (ii) not replaced. 
28. One bag contains 4 white and 2 black balls; another contains 3 white and 5 black balls. If one ball is drawn from each bag, find the probabilities that (i) both are white, (ii) both are black. 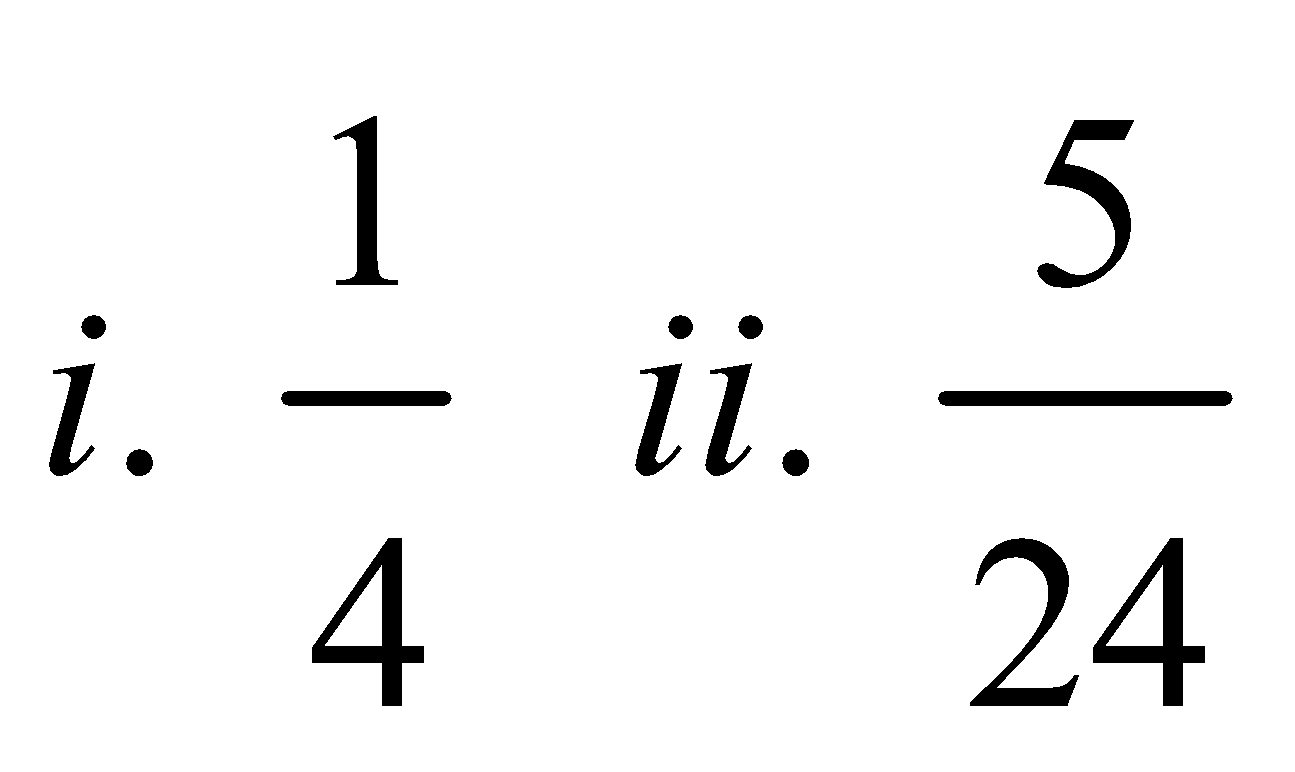
29. A box contains 8 tickets bearing numbers 1, 2, 3, 5, 7, 8, 9, 10. One ticket is drawn at random and kept aside, and then the second ticket is drawn. Find the probability that both the tickets show odd numbers. 
30. P can hit a target 4 times in 5 shots, Q, 3 times in 4 shots and R, twice in 3 shots. They fire simultaneously. What is the probability that at least 2 shots hit the target? 
31. A purse contains 2 silver coins and 4 copper coins and another contains 4 silver and 3 copper coins. If a coin is selected at random from any one of the two purses what is the probability that it is a silver coin? 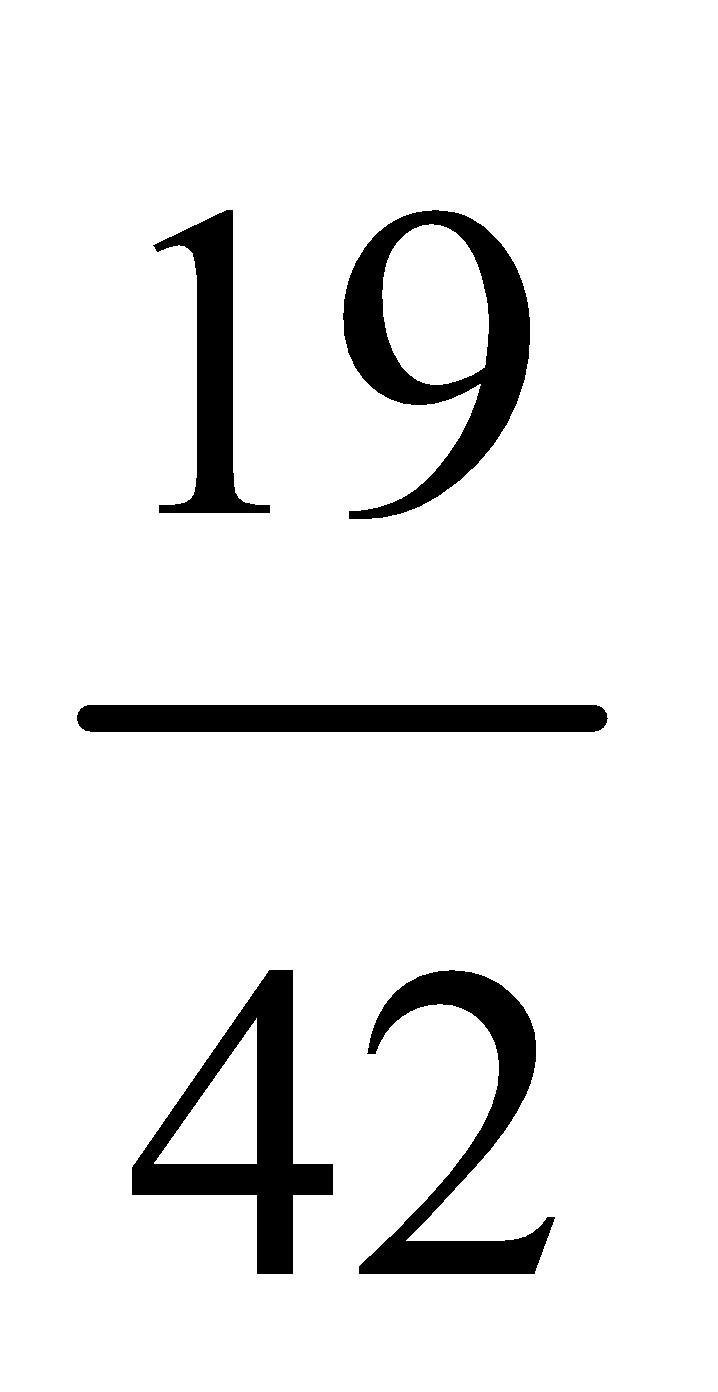
32. The probability that A can solve a problem is  that B can solve it is
that B can solve it is  and that C can solve it is
and that C can solve it is . If all of them try independently, find the probability that the problem will be solved?
. If all of them try independently, find the probability that the problem will be solved? 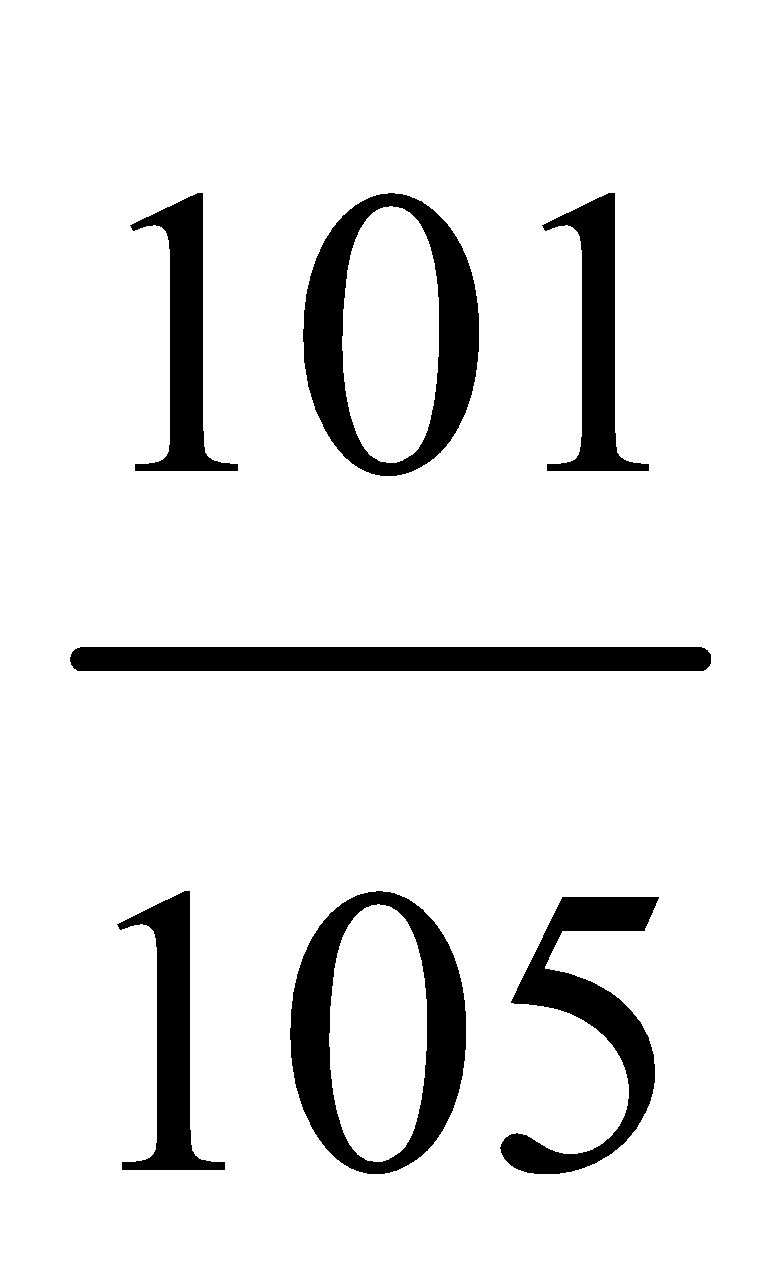
33. The odds that a book will be favourably reviewed by three independent critics are 3 to 2, 4 to 3 and 2 to 3. What is the probability that of the three reviews a majority will be favourable? 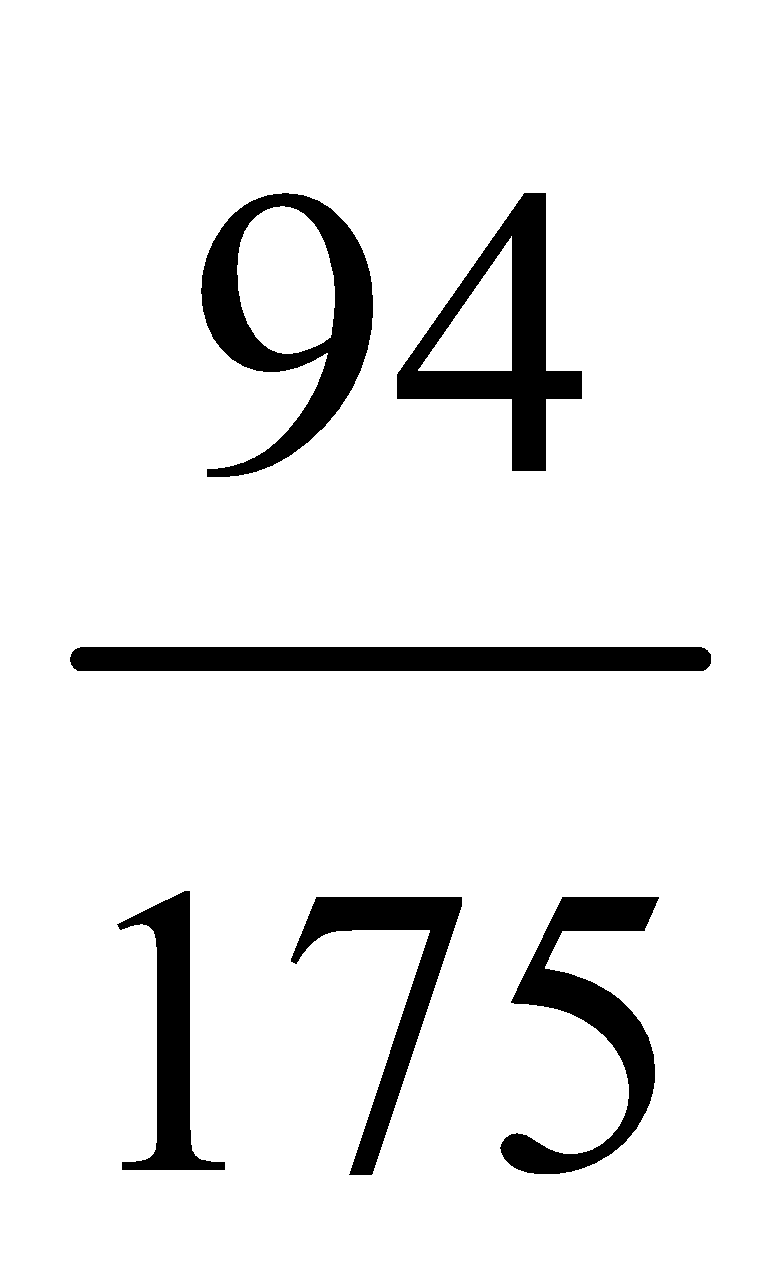
34. The odds against A solving a problem are 8 to 6 and odds in favour of B solving the same problem are 14 to 16. If both of them try the problem, what is the probability that (i) the problem will be solved, (ii) both A and B will solve the problem? 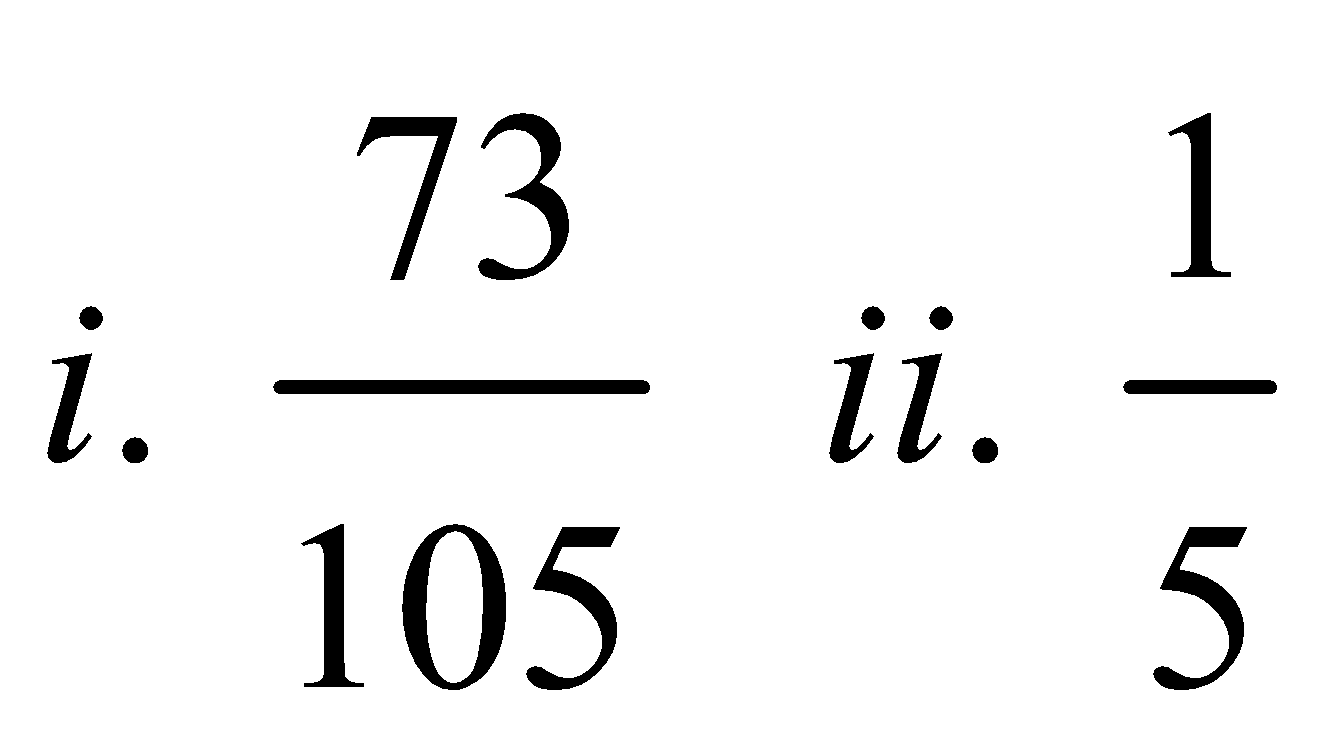
35. A and B play games of chess. A wins 6 times, B wins 4 times and 2 games are drawn. They, then agree to play 3 more games. Find the probability that (i) A wins all the three games (ii) 2 of the games end in a draw. 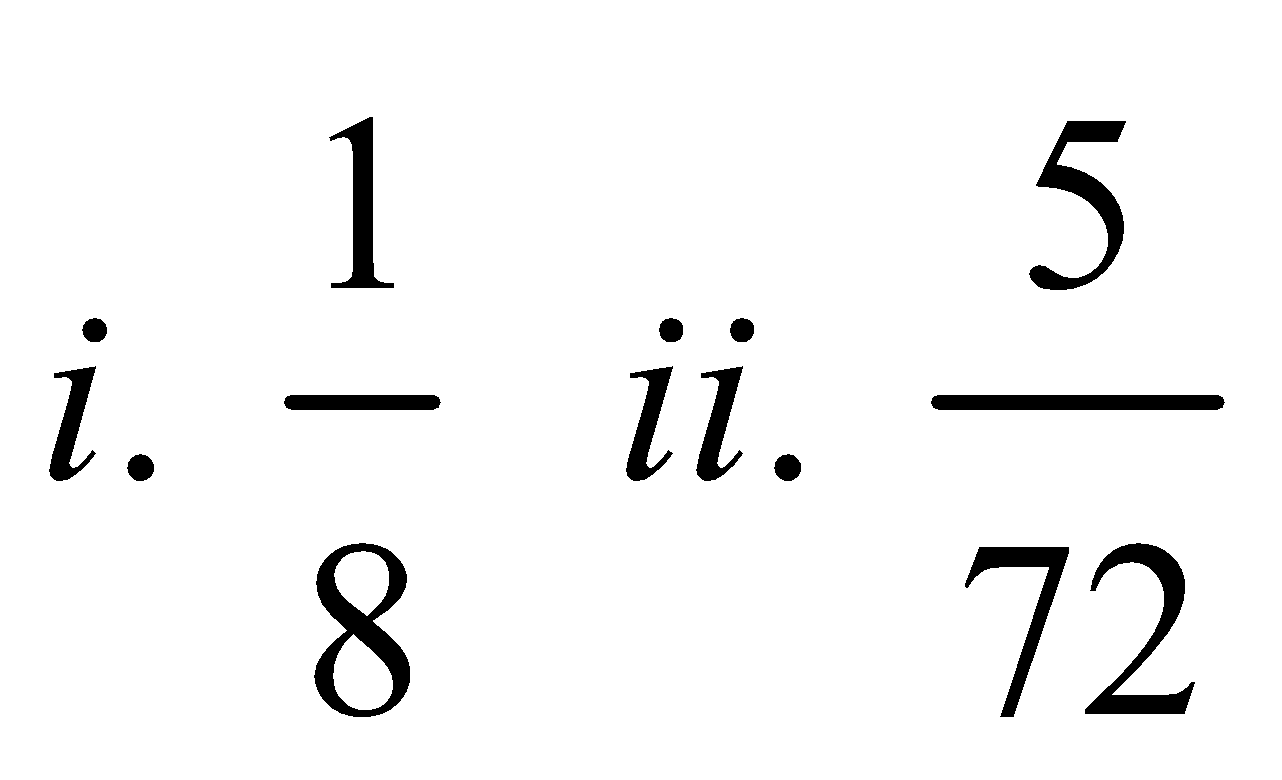
36. The probability that a 50-year old man will be alive at 60 is 0.83 and the probability that a 45-year old woman will be alive at 55 is 0.87. What is the probability that a man who is 50 and wife who is 45 will be alive 10 years hence? 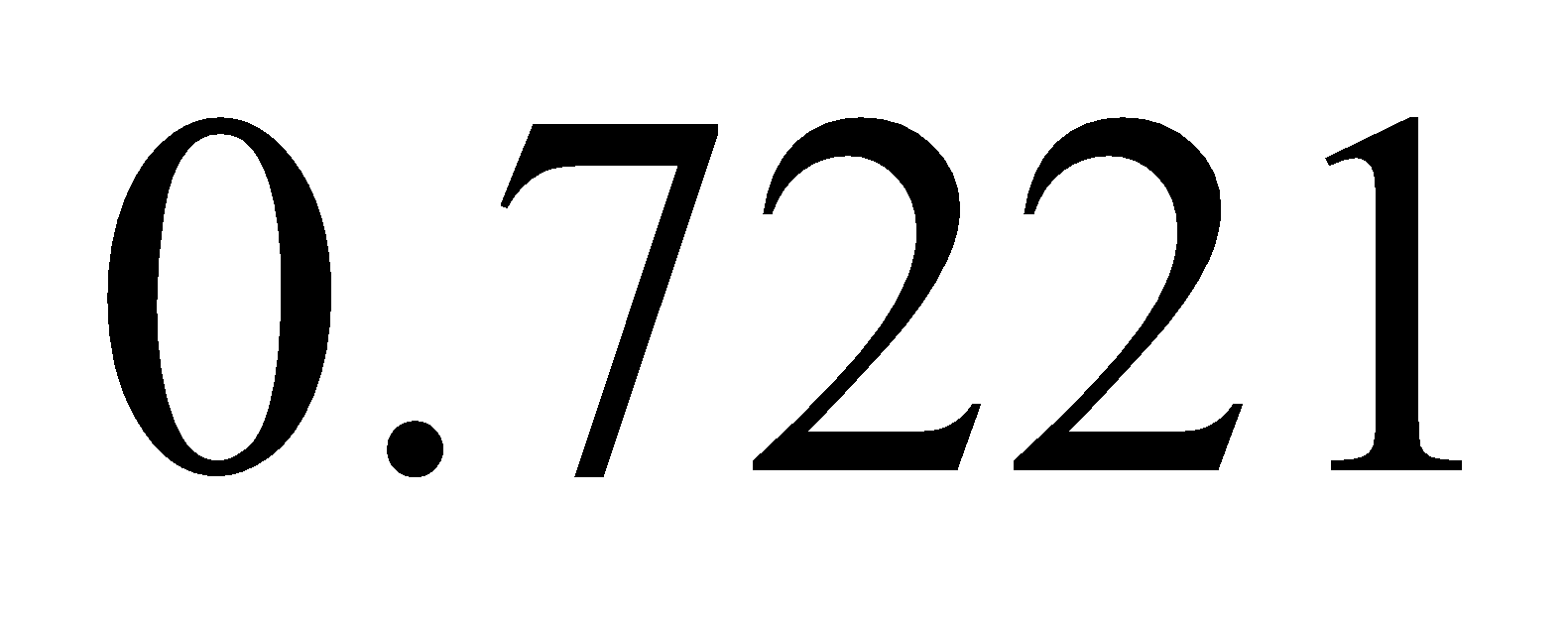
39. There are 50 tickets in a lottery in which there is a first and a second prize. What is the probability that a man possessing 5 tickets wins a prize? 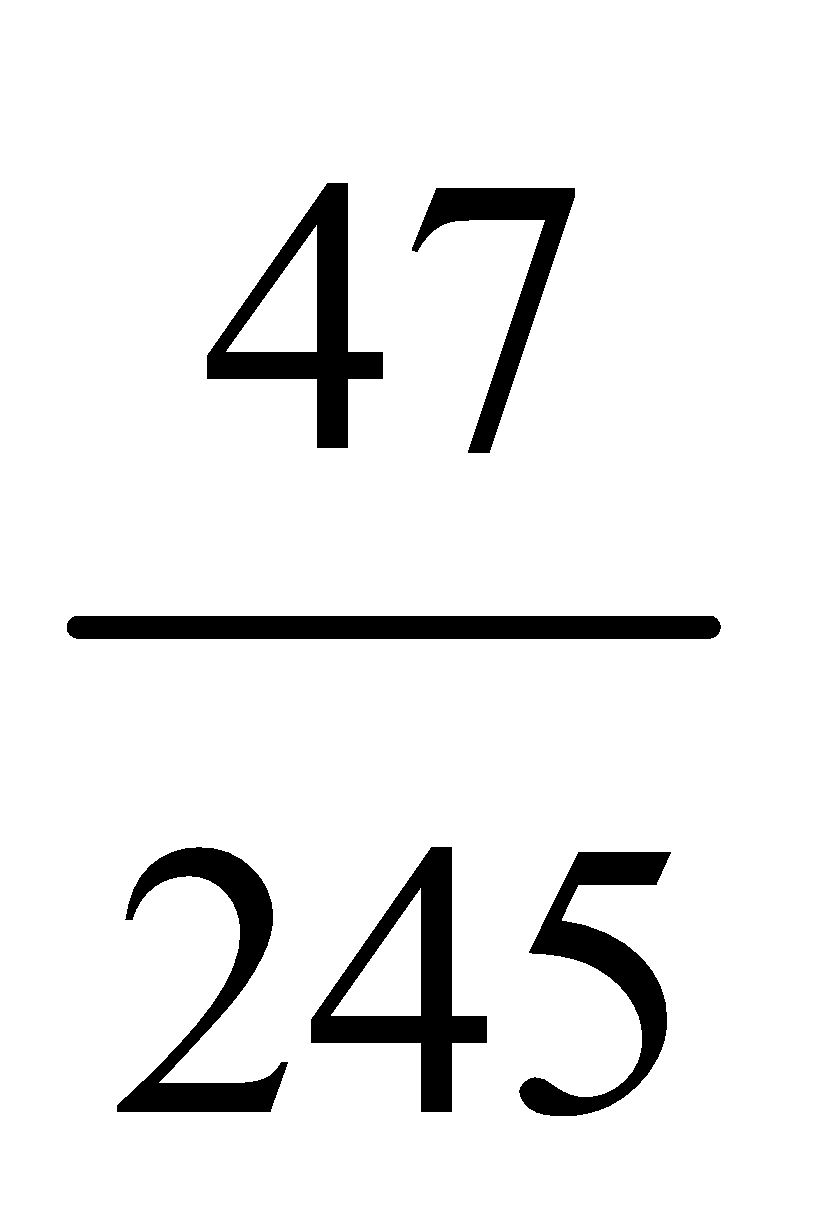
40. An urn contains four white and five black balls; a second urn contains five white and four black balls. One ball is transferred from the first to the second urn, and then a ball is drawn from the second urn. What is the probability that it is white in colour?