Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.7
Multiple Choice Questions
Question 1.
Which of the following is correct?
(1) {7} ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(2) 7 ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(3) 7 ∉ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(4) {7} ⊈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Solution:
(2) 7 ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Question 2.
The set P = {x | x ∈ Z, -1 < X < 1} is a
(1) Singleton set
(2) Power set
(3) Null set
(4) Subset
Solution:
(1) Singleton set
Hint: P = {0}
If U = {x | x ∈ N, x < 10} and A = {x | x ∈ N, 2 ≤ x < 6} then (A’)’ is
(1) {1, 6, 7, 8, 9}
(2) {1, 2, 3, 4}
(3) {2, 3, 4, 5}
(4) { }
Solution:
(3) {2, 3, 4, 5}
Hint: (A’) = A= {2, 3, 4, 5}
Question 4.
If B ⊆ A then n(A ∩ B) is
(1) n(A – B)
(2) n(B)
(3) n(B – A)
(4) n(A)
Solution:
(2) n(B)
Hint: B ⊆ A ⇒ A ∩ B = B
Question 5.
If A= {x, y, z} then the number of non-empty subsets of A is
(1) 8
(2) 5
(3) 6
(4) 7
Solution:
(4) 7
Hint: Number of non-empty subsets = 2 – 1 = 8 – 1 = 7
Question 6.
Which of the following is correct ?
(1) Ø ⊆ {a,b}
(2) Ø ∈ {a, b}
(3) {a} ∈ {a, b}
(4) a ⊆ {a, b}
Solution:
(1) Ø ⊆ {a,b}
Hint: Empty set is an improper subset
Question 7.
If A ∪ B = A ∩ B, then
(1) A ≠ B
(2) A = B
(3) A ⊂ B
(4) B ⊂ A
Solution:
(2) A = B
Question 8.
If B – A is B, then A ∩ B is
(1) A
(2) B
(3) U
(4) Ø
Solution:
(4) Ø
Hint: B – A = B ⇒ A and B are disjoint sets.
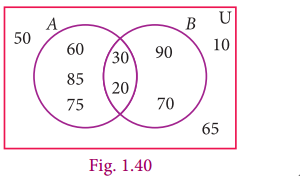
Question 9.
From the adjacent diagram n[P(A ∆ B) is
(1) 8
(2) 16
(3) 32
(4) 64
Solution:
(3) 32
Hint: A ∆ B = { 60, 85, 75, 90, 70}
⇒ n(A ∆ B) = 5
⇒ n(P(A ∆ B)) = 25 = 32
Question 10.
If n(A) = 10 and n(B) = 15 then the minimum and maximum number of elements in A ∩ B is
(1) (10, 15)
(2) (15, 10)
(3) (10, 0)
(4) (0, 10)
Solution:
(4) (0, 10)
Question 11.
Let A = {Ø} and B = P(A) then A ∩ B is
(1) {Ø, {Ø} }
(2) {Ø}
(3) Ø
(4) {0}
Solution:
(2) {Ø}
Hint: P(A) = {Ø {Ø}}
Question 12.
In a class of 50 boys, 35 boys play carom and 20 boys play chess then the number of boys play both games is
(1) 5
(2) 30
(3) 15
(4) 10
Solution:
(1) 5
Hint: n(A ∪ B) = n(A) + n(B) – n(A n B) ⇒ 50 = 35 + 20 – n(A ∩ B) ⇒ n(A ∩ B) = 5
Question 13.
If U = {x : x ∈ N and x < 10}, A = {1, 2, 3, 5, 8} and B = {2, 5, 6, 7, 9}, then n[(A ∪ B)’] is
(1) 1
(2) 2
(3) 4
(4) 8
Solution:
(1) 1
Hint: U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 5, 8}
B = {2, 5, 6, 7, 9}
A ∪ B = {1, 2, 3, 5, 6, 7, 8, 9}
(A ∪ B)’ = {4},
n(A ∪ B)’ = 1
Question 14.
For any three sets P, Q and R, P – (Q ∩ R) is
(1), P – (Q ∪ R)
(2) (P ∩ Q) – R
(3) (P – Q) ∪ (P – R)
(4) (P – Q) ∩ (P – R)
Solution:
(3) (P – Q) ∪ (P – R)
Hint: P – (Q ∩ R) = (P – Q) ∪ (P – R)
Question 15.
Which of the following is true?
(1) A – B = A ∩ B
(2) A – B = B – A
(3) (A ∪ B)’ = A’ ∪ B’
(4) (A ∩ B)’ = A’ ∪ B’
Solution:
(4) (A ∩ B)’ = A’ ∪ B’
Hint: (1) (A – B) = A ∩ B ✘
(2) A – B = B – A ✘
(3) (A ∪ B) = A’ ∪ B’ ✘
(4) (A ∩ B)’ = A’ ∪ B’ ✓
Question 16.
If n(A ∪ B ∪ C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ∩ C) = 15, n(A ∩ C) = 25 and n(A ∩ B ∩ C)= 10 , then the value of x is
(A) 10
(B) 15
(C) 25
(D) 30
Solution:
(A) 10
Hint:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
100 = 4x + 6x + 5x – 20 – 15 – 25 + 10
100 = 15x -60 + 10
100 = 15x – 50
∴ 15x = 100 + 50 = 150
x = 10
Question 17.
For any three sets A, B and C, (A – B) ∩ (B – C) is equal to
(1) A only
(2) B only
(3) C only
(4) ϕ
Solution:
(4) ϕ
Hint: (A – B) ∩ (B – C) is equal to Φ
Question 18.
If J = Set of three sided shapes, K = Set of shapes with two equal sides and L = Set of shapes with right angle, then J ∩ K ∩ L is
(1) Set of isoceles triangles
(2) Set of equilateral triangles
(3) Set of isoceles right triangles
(4) Set of right angled triangles
Solution:
(3) Set of isoceles right triangles
Hint:
Question 19.
The shaded region in the Venn diagram is
(1) Z – (X ∪ Y)
(2) (X ∪ Y) ∩ Z
(3) Z – (X ∩ Y)
(4) Z ∪ (X ∩ Y)
Answer:
(3) Z – (X ∩ Y)
Hint:
Z – (X ∩ Y)
Question 20.
In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
(1) 5
(2) 8
(3) 10
(4) 15
Answer:
(1) 5
Hint:
40 + 35 + 20 + x = 100%
95% + x = 100%
x = 5%