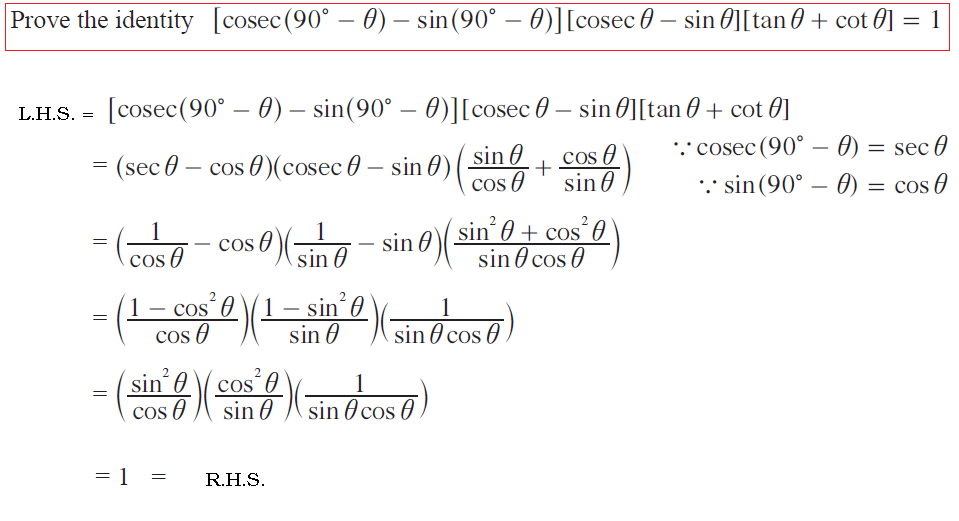MENSURATION FORMULAE

The angle of elevation of the top of a hill from the foot of a tower is 60 degree and the angle of elevation of the top of the tower from the foot of the hill is 30 degree. If the tower is 50 m high, then find the height of the hill.

A jet fighter at a eight of 3000 m from the ground, passes directly over another jet fighter at an instance when their angles of elevation from the same observation point are 60 degree and 45 degree respectively. Find the distance of the first jet fighter from the second jet at that instant.

A vertical tree is broken by the wind. The top of the tree touches the ground and makes an angle 30 degree with it. If the top of the tree touches the ground 30 m away from its foot, then find the actual height of the tree.

The angle of elevation of the top of a tower as seen by an observer is 30 degree. The observer is at a distance of 30√3m from the tower. if the eye level of the observer is 1.5m above the ground level, then find the height of the tower.

Find the angular elevation (angle of elevation from the ground level) of the sun when the length of the shadow of a 30m long pole is 10√3 m.

TRIGONOMETRY EXTRA HOTS FOR PRACTICE

The angle of elevation of the top of a hill from the foot of a tower is 60 degree and the angle of elevation of the top of the tower from the foot of the hill is 30 degree. If the tower is 50 m high, then find the height of the hill.

A jet fighter at a eight of 3000 m from the ground, passes directly over another jet fighter at an instance when their angles of elevation from the same observation point are 60 degree and 45 degree respectively. Find the distance of the first jet fighter from the second jet at that instant.

The angle of elevation of an aeroplane from a point A on the ground is 60 degree. After a flight of 15 seconds horizontally, the angle of elevation changes to 30 degree. If the aeroplane is flying at a speed of 200 m/s, then find the constant height at which the aeroplane is flying.

A flag post stands on the top of a building. From a point on the ground, the angles of elevation of the top and bottom of the flag post are 60 degree and 45 degree respectively. If the height of the flag post is 10 m, find the height of the building.

A boy spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground level. The distance of his eye level from the ground is 1.2 m. The angle of elevation of the balloon from his eyes at an instant is 60 degree. After some time, from the same point of observation, the angle of elevation of the balloon reduces to 30 degree. Find the distance covered by the balloon during the interval.

A girl standing on a lighthouse build on a cliff near the seashore, observes two boats due East of the lighthouse. The angles of depression of the two boats are 30 degree and 60 degree. The distance between the boats is 300 m. Find the distance of the top of the lighthouse from the sea level.

A vertical wall and a tower are on the ground. As seen from the top of the tower, the angles of depression of the top and bottom of the wall are 40 degree and 60 degree respectively. Find the height of the wall if the height of the tower is 90 m .

A vertical tree is broken by the wind. The top of the tree touches the ground and makes an angle 30 degree with it. If the top of the tree touches the ground 30 m away from its foot, then find the actual height of the tree.

The angle of elevation of the top of a tower as seen by an observer is 30 degree. The observer is at a distance of 30√3m from the tower. if the eye level of the observer is 1.5m above the ground level, then find the height of the tower.

Find the angular elevation (angle of elevation from the ground level) of the sun when the length of the shadow of a 30m long pole is 10√3 m.

A ladder leaning against a vertical wall, makes an angle of 60 degree with the ground. The foot of the ladder is 3.5 m away from the wall. Find the length of the ladder.

A kite is flying with a string of length 200 m. If the thread makes an angle of 300 with the ground, find the distance of the kite from the ground level. (Here, assume the string is along a straight line)

If tan^2 α = cos^2 β – sin^2 β , then prove that cos^2α – sin^2 α = tan^2 β

tanθ + sin θ = m, tanθ – sinθ = n and m is not equal to n, then show that m^2-n^2=4√mn.

Prove the identity (cosecθ – sinθ )(secθ – cosθ ) = 1/(tanθ + cotθ)

Prove that (1+secθ)/secθ = sin^2θ/(1-cosθ)

Prove the identity [(secθ – tanθ )/(secθ +tanθ)]=1- 2secθ tanθ + 2tan^2 θ

Prove the identity [(sinθ – 2sin^3θ )/(2cos^3θ –cosθ )] = tanθ

Prove the identity (sin^6θ + cos^6θ ) = 1 – 3sin^2 θ cos^2 θ

Prove the identity (sinθ +cosecθ )^2 + (Cosecθ +secθ )^2 = 7+tan^2 θ + cot^2 θ

Prove the identity [tanθ /(1-cotθ)]+[cotθ /(1-tanθ )] = 1+tanθ +cotθ

Prove that [(tanθ + secθ – 1)/(tanθ – secθ +1)] = [(1+sinθ )/cosθ )]

Prove the identity [cosec (90 - θ ) – sin(90 - θ ) [cosec θ – sinθ ][tanθ + cotθ ] = 1

Prove the identity √(1-cosθ )/√(1+cosθ) = cosecθ – cotθ

Prove the identity (sinθ /cosecθ) + (cosθ /secθ ) = 1

A ladder leaning against a vertical wall, makes an angle of 600 with the ground. The foot of the ladder is 3.5 m away from the wall. Find the length of the ladder.

A ladder leaning against a vertical wall, makes an angle of 60⁰ with the ground. The foot of the ladder is 3.5 m away from the wall. Find the length of the ladder.

Solution:

Let AC be the length of the ladder,

AB be the distance between the foot of the ladder and the base of the wall.

Thus, AB = 3.5 m  (Given)

In right angled triangle, ∆ ABC,

cos 60⁰ =  ^AB/_AC

∴¹/₂ = ^3.5/_AC

∴ AC = 3.5 × 2

∴ AC = 7 m.

∴  The length of the ladder is 7m. 

A kite is flying with a string of length 200 m. If the thread makes an angle of 300 with the ground, find the distance of the kite from the ground level. (Here, assume the string is along a straight line)

A kite is flying with a string of length 200 m. If the thread makes an angle of 30⁰ with the ground, find the distance of the kite from the ground level. (Here, assume the string is along a straight line)

Solution: 

Let h be the height of the kite from the ground level.

In, ∆ ABC, AC be the length of the string,

Given that ∠ CAB = 30⁰  and AC = 200 m.

In the right angled triangle, ∆ CAB

sin30⁰ = ^h/₂₀₀

∴ ½ = ^h/₂₀₀

_{∴ h =} ²⁰⁰/₂

_{∴ h = 100 m.}

_{Hence the height of the kite from the ground level is 100 m.} 

If tan^2 α = cos^2 β – sin^2 β , then prove that cos^2α – sin^2 α = tan^2 β

tanθ + sin θ = m, tanθ – sinθ = n and m is not equal to n, then show that m^2-n^2=4√mn.

Prove the identity (cosecθ – sinθ )(secθ – cosθ ) = 1/(tanθ + cotθ)

Prove that (1+secθ)/secθ = sin^2θ/(1-cosθ)

Prove the identity [(secθ – tanθ )/(secθ +tanθ)]=1- 2secθ tanθ + 2tan^2 θ

Prove the identity [(sinθ – 2sin^3θ )/(2cos^3θ –cosθ )] = tanθ

Prove the identity (sin^6θ + cos^6θ ) = 1 – 3sin^2 θ cos^2 θ

Prove the identity (sinθ +cosecθ )^2 + (Cosecθ +secθ )^2 = 7+tan^2 θ + cot^2 θ

Prove the identity [tanθ /(1-cotθ)]+[cotθ /(1-tanθ )] = 1+tanθ +cotθ

Prove that [(tanθ + secθ – 1)/(tanθ – secθ +1)] = [(1+sinθ )/cosθ )]

Prove the identity [cosec (90 - θ ) – sin(90 - θ ) [cosec θ – sinθ ][tanθ + cotθ ] = 1

Prove the identity √(1-cosθ )/√(1+cosθ) = cosecθ – cotθ

Prove the identity (sinθ /cosecθ) + (cosθ /secθ ) = 1

IMPORTANT THEOREMS GEOMETRY : SIMILARITY AND CIRCLE CHAPTER

If a line parallel to one side of a triangle intersects the other two sides in two distinct points, then the other two sides are divided in the same ratio by it.

The ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

The opposite angles of a cyclic quadrilateral are supplementary.

If a secant and a tangent of a circle intersect in a point outside the circle then the area of the rectangle formed by the two line segments corresponding to the secant is equal to the area of the square formed by line segment corresponding the tangent.

The lengths of the two tangents segments to a circle drawn from an external point are equal.

If the angles of a triangle are 45 degree, 45 degree, and 90 degree, then each of the perpendicular sides is (1/√2 ) times the hypotenuse.

Similarity Extra HOTS for Practice with solution

In ∆ PQR, AB || QR. If AB is 3 cm, PB is 2 cm and PR is 6 cm, then find the length of of QR.

 

D is the midpoint of the side BC of ∆ ABC. If P and Q are points on AB and on AC such that DP bisects ∠BDA and DQ bisects ∠ADC, then prove that PQ || BC.

 

In ∆ ABC, AE is the external bisector of ∠A, meeting BC produced at E. If AB = 10 cm, AC = 6 cm and BC = 12 cm, then find CE.

 

In ∆ ABC, the internal bisector AD of ∠ A meets the side BC at D. If BD = 2.5cm, AB = 5 cm and AC = 4.2 cm, then find DC.

 

In triangle ABC, points D, E and F are taken on the sides AB, BC and CA respectively such that DE || AC and FE || AB.

 

In triangle PQR, given that S is a point on PQ such that ST is parallel to QR and PA:SQ = 3:5, If PR = 5.6 cm, then find PT.

 

In Triangle ABC. DE is parallel to BC and AD:DB = 2:3, IF AE = 3.7 cm, Find EC.

In ∆ PQR, AB || QR. If AB is 3 cm, PB is 2 cm and PR is 6 cm, then find the length of of QR.

D is the midpoint of the side BC of ∆ ABC. If P and Q are points on AB and on AC such that DP bisects ∠BDA and DQ bisects ∠ADC, then prove that PQ || BC.

In ∆ ABC, AE is the external bisector of ∠A, meeting BC produced at E. If AB = 10 cm, AC = 6 cm and BC = 12 cm, then find CE.

In ∆ ABC, the internal bisector AD of ∠ A meets the side BC at D. If BD = 2.5cm, AB = 5 cm and AC = 4.2 cm, then find DC.

In triangle ABC, points D, E and F are taken on the sides AB, BC and CA respectively such that DE || AC and FE || AB.