Laws Of Motion
Class 9th Science & Technology MHB Solution
Chapter Exercises
- Match columns and remake the table.
- Clarify differences: Distance and displacement.
- Clarify differences: Uniform and non-uniform motion.
- Complete the following tables.
- Complete the sentences and explain them.
- Scientific reason: Uniform acceleration in free fall.
- Scientific reason: Action-reaction forces don't cancel.
- Scientific reason: Easier to stop a tennis ball than a cricket ball.
- Scientific reason: Velocity of an object at rest.
- Examples of Newton's laws from surroundings.
- Problem: Calculate average speed of an object.
- Problem: Calculate applied force and acceleration.
- Problem: Bullet and plank velocity after collision.
- Problem: Calculate average speed of a swimmer.
Detailed Solutions
Match the first column with appropriate entries in the second and third columns and remake the table.
| Column I | Column II | Column III |
|---|---|---|
| Negative acceleration | The velocity of the object decreases | A vehicle moving with a velocity of 10 m/s stops after 5 s. |
| Positive acceleration | The velocity of the object increases | A car, initially at rest reaches a velocity of 10 m/s in 5 s. |
| Zero acceleration | The velocity of the object is constant | A vehicle is moving with a velocity of 10 m/s. |
The corresponding velocity-time graphs are given below:
Clarify the differences: Distance and displacement.
| Basis of Difference | Distance | Displacement |
|---|---|---|
| Definition | The total length of the path covered by an object during its motion. | The shortest distance between the initial and final positions of an object. |
| Nature | It is a scalar quantity (only has magnitude). | It is a vector quantity (has both magnitude and direction). |
| Value | Always positive or zero. It can never be negative. | Can be positive, negative, or zero. |
| Path Dependence | Depends on the path taken by the object. | Does not depend on the path taken; only on start and end points. |
In the diagram, the curved path (ACDB) represents the distance, while the straight line (AB) represents the displacement.
Clarify the differences: Uniform and non-uniform motion.
| Basis of Difference | Uniform Motion | Non-uniform Motion |
|---|---|---|
| Definition | An object covers equal distances in equal intervals of time. | An object covers unequal distances in equal intervals of time. |
| Velocity | Velocity is constant (speed and direction do not change). | Velocity is variable (either speed, direction, or both change). |
| Acceleration | Acceleration is zero. | Acceleration is non-zero (it can be positive or negative). |
| Distance-Time Graph | A straight line. | A curved line. |
Graphical Representation:
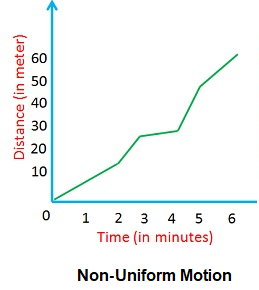
Complete the following tables.
The calculations are based on the three equations of motion:
- v = u + at
- s = ut + ½ at2
- v2 = u2 + 2as
Table 1 (using v = u + at):
| u (m/s) | a (m/s2) | t (s) | v (m/s) |
|---|---|---|---|
| 2 | 4 | 3 | 14 |
| 10 | 5 | 2 | 20 |
Table 2 (using s = ut + ½ at2):
| u (m/s) | a (m/s2) | t (s) | s (m) |
|---|---|---|---|
| 5 | 12 | 3 | 69 |
| 7 | 8 | 4 | 92 |
Table 3 (using v2 = u2 + 2as):
| u (m/s) | a (m/s2) | s (m) | v2 (m2/s2) |
|---|---|---|---|
| 4 | 3 | -1.33 | 8 |
| 8.6 | 5 | 8.4 | 100 |
Note: The calculations for the third table result in a negative displacement (s) and a real value for initial velocity (u) derived from a negative square, which might indicate an error in the original problem's values. The mathematical results are provided as calculated. For u2 = -74, u would be imaginary. Assuming v2 was 10, not v=10, then u = sqrt(100-84) = 4 m/s. We have assumed v=10, thus v2=100.
Complete the sentences and explain them.
A. The minimum distance between the start and finish points of the motion of an object is called the ______ of the object.
B. Deceleration is ______ acceleration.
C. When an object is in uniform circular motion, its ______ changes at every point.
D. During collision ______ remains constant.
E. The working of a rocket depends on Newton’s ______ law of motion.
A. The minimum distance between the start and finish points of the motion of an object is called the displacement of the object.
Explanation: Displacement is the straight-line path from the starting point to the ending point, regardless of the actual path traveled. It is the shortest possible distance.
B. Deceleration is negative acceleration.
Explanation: Acceleration is the rate of change of velocity. If the velocity is increasing, acceleration is positive. If the velocity is decreasing, the rate of change is negative, which is known as deceleration or retardation.
C. When an object is in uniform circular motion, its velocity changes at every point.
Explanation: In uniform circular motion, the speed (magnitude of velocity) is constant, but the direction of motion is continuously changing. Since velocity is a vector quantity (speed + direction), a change in direction means the velocity is changing.
D. During collision total momentum remains constant.
Explanation: This is the principle of conservation of momentum. In a closed system (with no external forces), the total momentum of the objects before a collision is equal to the total momentum of the objects after the collision.
E. The working of a rocket depends on Newton’s third law of motion.
Explanation: Newton's third law states that for every action, there is an equal and opposite reaction. A rocket expels hot gases downwards (action). In reaction, the gases exert an equal and opposite upward force on the rocket, propelling it into the sky.
Give scientific reasons: When an object falls freely to the ground, its acceleration is uniform.
When an object falls freely, the only force acting on it is Earth's gravity (ignoring air resistance). According to Newton's second law, Force = mass × acceleration (F=ma). The gravitational force is given by F = (GMm)/r2, where G is the gravitational constant, M is the mass of the Earth, m is the mass of the object, and r is the distance to the Earth's center.
Therefore, ma = (GMm)/r2. The mass of the object 'm' cancels out, leaving a = GM/r2.
For objects falling near the Earth's surface, the distance 'r' is approximately equal to the Earth's radius, which is very large and essentially constant. Since G, M, and r are all constant, the acceleration 'a' (also known as 'g', the acceleration due to gravity) is uniform and approximately 9.8 m/s2.
Give scientific reasons: Even though the magnitudes of action force and reaction force are equal and their directions are opposite, their effects do not get cancelled.
Action and reaction forces, as described by Newton's third law, do not cancel each other out because they act on different objects.
- Forces on Different Bodies: An action force is exerted by object A on object B, while the reaction force is exerted by object B on object A. To cancel forces, they must act on the same object.
- Example: When you push a wall (action: your hand on the wall), the wall pushes back on you (reaction: wall on your hand). The force on the wall may not be enough to move it, but the force on you is felt. Since the forces are on different bodies (wall and hand), they cannot be added together to get zero.
Give scientific reasons: It is easier to stop a tennis ball as compared to a cricket ball, when both are travelling with the same velocity.
This difference is due to the concept of momentum. Momentum (p) is the product of an object's mass (m) and its velocity (v), i.e., p = mv.
- Mass Difference: A cricket ball has significantly more mass than a tennis ball.
- Momentum Difference: Since both balls are traveling at the same velocity, the more massive cricket ball has a much higher momentum than the tennis ball.
- Force Required: To stop an object, a force must be applied to change its momentum to zero. According to Newton's second law, Force is the rate of change of momentum. A larger momentum requires a larger force (or the same force for a longer time) to stop. Therefore, it is easier to stop the tennis ball because it has less momentum.
Give scientific reasons: The velocity of an object at rest is considered to be uniform.
Uniform velocity means that the velocity is constant; it does not change over time. An object at rest has a velocity of zero. As time passes, if the object remains at rest, its velocity continues to be zero.
Since the velocity (zero) is not changing, it fits the definition of uniform velocity. Therefore, being at rest is a special case of motion with uniform (constant) velocity.
Take 5 examples from your surroundings and give explanation based on Newton's laws of motion.
1. Newton's First Law (Inertia): A book on a table will stay there until someone picks it up.
Explanation: The book is at rest and will remain at rest (due to inertia) unless an external unbalanced force (like your hand) acts on it.
2. Newton's First Law (Inertia): When a bus suddenly stops, passengers lurch forward.
Explanation: The passengers' bodies were in motion along with the bus. When the bus stops, their bodies tend to continue moving forward due to inertia.
3. Newton's Second Law (F=ma): It's easier to push an empty shopping cart than a full one.
Explanation: The full cart has more mass. To achieve the same acceleration, you must apply a greater force (F=ma).
4. Newton's Third Law (Action-Reaction): A person swimming pushes water backward.
Explanation: The swimmer pushes the water backward (action). The water pushes the swimmer forward with an equal and opposite force (reaction), causing them to move.
5. Newton's Third Law (Action-Reaction): A bird flies by pushing air downwards with its wings.
Explanation: The bird's wings push air down (action). The air pushes the bird up (reaction), providing the lift needed to fly.
Solve the following example: An object moves 18 m in the first 3 s, 22 m in the next 3 s and 14 m in the last 3 s. What is its average speed?
Average speed is calculated as the total distance traveled divided by the total time taken.
Total Distance = 18 m + 22 m + 14 m = 54 m
Total Time = 3 s + 3 s + 3 s = 9 s
Average Speed = Total Distance / Total Time
Average Speed = 54 m / 9 s = 6 m/s
Solve the following example: An object of mass 16 kg is moving with an acceleration of 3 m/s2. Calculate the applied force. If the same force is applied on an object of mass 24 kg, how much will be the acceleration?
Part 1: Calculate the applied force.
Using Newton's second law: Force (F) = mass (m) × acceleration (a)
Given: m = 16 kg, a = 3 m/s2
F = 16 kg × 3 m/s2 = 48 N
Part 2: Calculate the new acceleration.
Now, the same force (48 N) is applied to a new mass.
Given: F = 48 N, m = 24 kg
Rearranging the formula: a = F / m
a = 48 N / 24 kg = 2 m/s2
Solve the following example: A bullet having a mass of 10 g and moving with a speed of 1.5 m/s, penetrates a thick wooden plank of mass 90 g. The plank was initially at rest. The bullet gets embedded in the plank and both move together. Determine their velocity.
This is a problem of inelastic collision, solved using the law of conservation of momentum.
Initial State (before collision):
- Mass of bullet (m1) = 10 g = 0.01 kg
- Velocity of bullet (u1) = 1.5 m/s
- Mass of plank (m2) = 90 g = 0.09 kg
- Velocity of plank (u2) = 0 m/s (at rest)
Initial Momentum = (m1u1) + (m2u2) = (0.01 kg × 1.5 m/s) + (0.09 kg × 0 m/s) = 0.015 kg·m/s
Final State (after collision):
- The bullet and plank move together, so their masses combine.
- Total Mass (M) = m1 + m2 = 0.01 kg + 0.09 kg = 0.1 kg
- Let their common final velocity be 'v'.
Final Momentum = M × v = 0.1 kg × v
Conservation of Momentum:
Initial Momentum = Final Momentum
0.015 kg·m/s = 0.1 kg × v
v = 0.015 / 0.1
v = 0.15 m/s
Solve the following example: A person swims 100 m in the first 40 s, 80 m in the next 40 s and 45 m in the last 20 s. What is the average speed?
Average speed is calculated as the total distance traveled divided by the total time taken.
Total Distance = 100 m + 80 m + 45 m = 225 m
Total Time = 40 s + 40 s + 20 s = 100 s
Average Speed = Total Distance / Total Time
Average Speed = 225 m / 100 s = 2.25 m/s